Додекаэдральные соты порядка 4

Додекаэдральные соты порядка 4
Тип	Гиперболические правильные соты
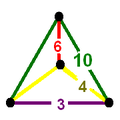
Символ Шлефли	{5,3,4} {5,31,1}
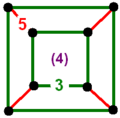
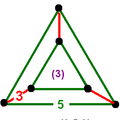
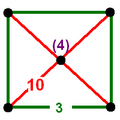
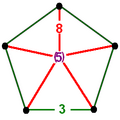
Диаграммы Коксетера — Дынкина	↔
Ячейки	{5,3}
Грани	Пятиугольники {5}
Рёберная фигура	квадраты {4}
Вершинная фигура	Октаэдр
Двойственные соты	Кубические соты порядка 5[англ.]
Группа Коксетера	BH3, [5,3,4] DH3, [5,31,1]
Свойства	Regular, квазиправильные соты

В гиперболическом трёхмерном пространстве додекаэдральные соты порядка 4 — это одна из четырёх компактных правильных заполняющих пространство мозаик (или сот). Имея символ Шлефли {5,3,4}, соты имеют четыре додекаэдра вокруг каждого ребра и 8 додекаэдров вокруг каждой вершины в октаэдральном расположении. Вершины сот строятся на 3 ортогональных осях. Двойственным телом сот являются кубические соты порядка 5^[англ.].

Геометрические соты — это таким образом заполняющие пространство многогранные ячейки, что не остаётся свободных промежутков. Соты являются примером более общего математического понятия замощения в пространствах любой размерности.

Соты обычно строятся в обычном евклидовом («плоском») пространстве подобно выпуклым однородным сотам^[англ.]. Они могут быть построены также в неевклидовых пространствах, такие как гиперболические однородные соты^[англ.]. Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы образовать однородные соты на сферическом пространстве.

Двугранный угол додекаэдра равен ~116.6°, так что невозможно разместить 4 додекаэдра на ребре в евклидовом 3-мерном пространстве. Однако в гиперболическом пространстве для додекаэдра можно подобрать размер так, что его двугранные углы уменьшаются до 90 градусов, а тогда четыре додекаэдра точно заполняют пространство вокруг каждого ребра.

Соты строятся с половинной симметрией, {5,3^1,1}, с двумя типами (цветами) шестиугольных мозаик в построении Витхоффа. ↔ .

Модель Бельтрами — Клейна

Существует четыре вида правильных компактных сот в гиперболическом 3D-пространстве:

Четыре вида правильных компактных сот в H³

{5,3,4}

{4,3,5}

{3,5,3}

{5,3,5}

Существует пятнадцать видов однородных сот^[англ.] в семействе [5,3,4] групп Коксетера, включая эти правильные формы.

Семейство сот [5,3,4]

{5,3,4}	r{5,3,4}	t{5,3,4}	rr{5,3,4}	t0,3{5,3,4}	tr{5,3,4}	t0,1,3{5,3,4}	t0,1,2,3{5,3,4}
{4,3,5}	r{4,3,5}	t{4,3,5}	rr{4,3,5}	2t{4,3,5}	tr{4,3,5}	t0,1,3{4,3,5}	t0,1,2,3{4,3,5}

Существует одиннадцать видов однородных сот^[англ.] в разветвлённом семействе [5,3^1,1] групп Коксетера, включая соты в чередующейся форме. Это построение может быть представлено чередованием (как на шахматной доске) с двумя цветами додекаэдральных ячеек.

Эти соты связаны также с 16-ячейником, кубическими сотами и шестиугольными мозаичными сотами порядка 4^[англ.], все имеют октаэдральные вершинные фигуры:

Правильные соты {p,3,4}
Пространство	S3	E3	H3
Вид	Конечные	Аффинные	Компактные	Паракомпактные	Неокомпактные
Название	{3,3,4}	{4,3,4}	{5,3,4}	{6,3,4}	{7,3,4}	{8,3,4}	... {∞,3,4}
Рисунок
Ячейки	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Эти соты являются частью последовательности четырёхмерных многогранников и сот с додекаэдральными ячейками:

{5,3,p}

Пространство	S3	H3
Вид	Конечные	Компактные		Паракомпактные	Неокомпактные
Название	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	... {5,3,∞}
Рисунок
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Полноусечённые додекаэдральные соты порядка 4
Тип	Однородные соты в гиперболическом пространстве[англ.]
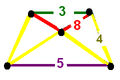
Символ Шлефли	r{5,3,4} r{5,31,1}
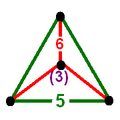
Диаграммы Коксетера — Дынкина	↔
Ячейки	r{5,3} {3,4}
Грани	Треугольники {3} пятиугольники {5}
Вершинная фигура	куб
Группа Коксетера	BH3, [5,3,4] DH3, [5,31,1]
Свойства	Вершинно транзитивные, рёберно транзитивные

Полноусечённые додекаэдральные соты порядка 4', , имеют чередующиеся октаэдральные и икосододекаэдральные ячейки с кубом в качестве вершинной фигуры.

Существует четыре вида полноусечённых компактных правильных сот:

Четыре полноусечённых правильных компактных сот в H³

Рисунок
Обозначение	r{5,3,4}	r{4,3,5}	r{3,5,3}	r{5,3,5}
Вершинная фигура

Усечённые додекаэдральные соты порядка 4
Тип	Однородные соты в гиперболическом пространстве[англ.]
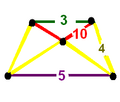
Символ Шлефли	t{5,3,4} t{5,31,1}
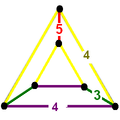
Диаграммы Коксетера — Дынкина	↔
Ячейки	t{5,3} {3,4}
Грани	Треугольники {3} десятиугольники {10}
Вершинная фигура	Квадратная пирамида
Группа Коксетера	BH3, [5,3,4] DH3, [5,31,1]
Свойства	Вершинно транзитивные

Усечённые додекаэдральные соты порядка 4, , имеют октаэдральные и усечённые додекаэдральные ячейки с кубом в качестве вершинной фигуры.

Соты можно рассматривать как аналог двумерных гиперболических усечённых пятиугольных мозаик порядка 4^[англ.] t{5,4} с гранями в виде усечённых пятиугольников и квадратов:

Четыре вида усечённых правильных правильных компактных сот в H³

Рисунок
Обозначение	t{5,3,4}	t{4,3,5}	t{3,5,3}	t{5,3,5}
Вершинная фигура

Биусечённые додекаэдральные соты порядка 4 Биусечённые кубические соты порядка 5
Тип	Однородные соты в гиперболическом пространстве[англ.]
Символ Шлефли	2t{5,3,4} 2t{5,31,1}
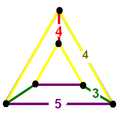
Диаграммы Коксетера — Дынкина	↔
Ячейки	t{3,5} t{3,4}
Грани	Треугольники {3} квадраты {4} шестиугольники {6}
Вершинная фигура	Тетраэдр
Группа Коксетера	BH3, [5,3,4] DH3, [5,31,1]
Свойства	Вершинно транзитивные

Биусечённые додекаэдральные соты порядка 4 или биусечённые кубические соты порядка 5, , имеют усечённые октаэдры и усечённые икосаэдры в качестве ячеек и тетраэдр в качестве вершинной фигуры.

Три вида биусечённых правильных компактных сот в H³

Рисунок
Обозначение	2t{4,3,5}	2t{3,5,3}	2t{5,3,5}
Вершинная фигура

Скошенные додекаэдральные соты порядка 4
Тип	Однородные соты в гиперболическом пространстве[англ.]
Символ Шлефли	rr{5,3,4} rr{5,31,1}
Диаграммы Коксетера — Дынкина	↔
Ячейки	rr{3,5} r{3,4} {}x{4} куб
Грани	Треугольники {3} квадраты {4} пятиугольники {5}
Вершинная фигура	Треугольная призма
Группа Коксетера	BH3, [5,3,4] DH3, [5,31,1]
Свойства	Вершинно транзитивные

Скошенные додекаэдральные соты порядка 4,, имеют ромбоикосододекаэдральные, кубооктаэдральные и кубические ячейки и треугольную призму в качестве вершинной фигуры.

Четыре вида скошенных правильных компактных сот в H3
Рисунок Обозначение rr{5,3,4} rr{4,3,5} rr{3,5,3} rr{5,3,5} Вершинная фигура

Скошено-усечённые додекаэдральные соты порядка 4
Тип	Однородные соты в гиперболическом пространстве[англ.]
Символ Шлефли	tr{5,3,4} tr{5,31,1}
Диаграммы Коксетера — Дынкина	↔
Ячейки	tr{3,5} t{3,4} {}x{4} Кубы
Грани	квадраты {4} шестиугольники {6} десятиугольники {10}
Вершинная фигура	зеркальный сфеноид
Группа Коксетера	BH3, [5,3,4] DH3, [5,31,1]
Свойства	Вершинно транзитивные

Скошено-усечённые додекаэдральные соты порядка 4 являются однородными сотами с диаграммой Коксетера — Дынкина и имеющие зеркальный сфеноид в качестве вершинной фигуры.

Четыре вида скошено-усечённых правильных компактных сот в H³

Рисунок
Обозначение	tr{5,3,4}	tr{4,3,5}	tr{3,5,3}	tr{5,3,5}
Вершинная фигура

Струг-усечённые додекаэдральные соты порядка 4
Тип	Однородные соты в гиперболическом пространстве[англ.]
Символ Шлефли	t0,1,3{5,3,4}
Диаграммы Коксетера — Дынкина
Ячейки	t{5,3} rr{3,4} {}x{10} {}x{4}
Грани	Треугольники {3} квадраты {4} десятиугольники {10}
Вершинная фигура	quad пирамида
Группа Коксетера	BH3, [5,3,4]
Свойства	Вершинно транзитивные

Струг-усечённые додекаэдральные соты порядка 4 — однородные соты с диаграммой Коксетера — Дынкина и четырёхугольной пирамидой в качестве вершинной фигуры.

Четыре вида струг-усечённых правильных компактных сот в H3
Рисунок Обозначение t0,1,3{5,3,4} t0,1,3{4,3,5} t0,1,3{3,5,3} t0,1,3{5,3,5} Вершинная фигура

• Выпуклые однородные соты в гиперболическом пространстве^[англ.]
• Poincaré homology sphere Poincaré dodecahedral space
• пространство Зейферта — Вебера^[англ.] Seifert–Weber dodecahedral space
• Список правильных многомерных многогранников и соединений

У этой статьи есть несколько проблем, помогите их исправить: Необходимо проверить качество перевода c неуказанного языка, исправить содержательные и стилистические ошибки. Вы можете помочь улучшить эту статью (см. также рекомендации по переводу). Оригинал не указан. Пожалуйста, укажите его. (26 сентября 2017) Стиль этой статьи неэнциклопедичен или нарушает нормы литературного русского языка. Статью следует исправить согласно стилистическим правилам Википедии. (26 сентября 2017) Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником.