| Восьмиугольная мозаика
|

|
| Тип |
Правильная гиперболическая мозаика
|
| Конфигурация вершины |
83
|
| Символ Шлефли |
{8,3}
t{4,8}
|
| Символ Витхоффа |
3 | 8 2
2 8 | 4
4 4 4 |
|
| Симметрии |
[8,3], (*832)
[8,4], (*842)
[(4,4,4)], (*444)
|
| Диаграммы Коксетера — Дынкина |
    
    
   
|
| Двойственные соты |
Треугольная мозаика порядка 8
|
| Свойства |
Изогональная, изотоксальная, изоэдральная
|
Восьмиугольная мозаика — это правильная мозаика на гиперболической плоскости.
Мозаика представлена символом Шлефли {8,3} и имеет три правильных восьмиугольник вокруг каждой вершины.
Мозаика также имеет построение в виде усечения квадратной мозаики порядка 8, t{4,8}.
Однородные раскраски
Подобно шестиугольной раскраске евклидовой плоскости имеется 3 такие однородные гиперболические раскраски.
Двойственная мозаика V8.8.8 представляет фундаментальные области с симметрией [(4,4,4)].
| Правильные
|
Усечения
|

{8,3}
    
|

t{4,8}
    
|

t{4[3]}
     = =      = =    
|
| Двойственная раскраска
|

{3,8}
     = =     
|

     = =    
|

     = =      = =       
|
Правильные карты
Правильную карту {8,3}2,0 можно рассматривать как 6-цветную раскраску гиперболической мозаики {8,3}.
В правильной карте восьмиугольники одного цвета считаются теми же гранями, показанными в разных местах.
Нижний индекс 2,0 показывает, что тот же цвет повторяется при движении на пару шагов в сторону противоположного ребра.
Эта правильная карта имеет также представление как двойное покрытие куба, что соответствует символу Шлефли {8/2,3},
с 6 восьмиугольными гранями, дважды обёрнутыми {8/2}, с 24 рёбрами и 16 вершинами.
Покрытие описано Бранко Грюнбаумом в главе Are Your Polyhedra the Same as My Polyhedra? (Ваш многогранник тот же, что и мой?) книги 2003 года[1]

Связанные многогранники и мозаики
Эта мозаика топологически является частью последовательности правильных многогранников и мозаик с символом Шлефли {n,3}.
*n32 варианты симметрии правильных мозаик: n3 или {n,3}
| Сферические
|
Евклидовы
|
Компактные
гиперболические.
|
Параком-
пактные.
|
Некомпактные гиперболические.
|

|

|

|

|

|

|

|

|
|

|

|

|
| {2,3}
|
{3,3}
|
{4,3}
|
{5,3}
|
{6,3}
|
{7,3}
|
{8,3}
|
{∞,3}
|
{12i,3}
|
{9i,3}
|
{6i,3}
|
{3i,3}
|
Она также топологически является частью последовательности правильных мозаик с символом Шлефли {8,n}.
Шаблон:Восьмиугольные мозаики
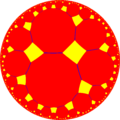
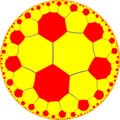
Исходя из построения Витхоффа существует десять гиперболических однородных мозаик,
которые базируются на правильных восьмиугольных мозаиках.
Если рисовать мозаики, выкрашивая красным цветом исходные грани, жёлтым цветом исходные вершины и синим цветом исходные рёбра,
получим 10 форм.
| Однородные восьмиугольные/треугольные мозаики
|
| Симметрия: [8,3], (*832)
|
[8,3]+
(832)
|
[1+,8,3]
(*443)
|
[8,3+]
(3*4)
|
| {8,3}
|
t{8,3}
|
r{8,3}
|
t{3,8}
|
{3,8}
|
rr{8,3}
s2{3,8}
|
tr{8,3}
|
sr{8,3}
|
h{8,3}
|
h2{8,3}
|
s{3,8}
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
|
|
    
|
|
|
|
    
   
|
    
   
|
|
    
|
|
|
    
    or or    
|
    
    or or    
|
    
   
|

|

|


|


|

|

|

|

|
 
|
 
|


|
| Однородные двойственные
|
| V83
|
V3.16.16
|
V3.8.3.8
|
V6.6.8
|
V38
|
V3.4.8.4
|
V4.6.16
|
V34.8
|
V(3.4)3
|
V8.6.6
|
V35.4
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|

|

|

|

|

|

|
|

|

|

|
| Однородные восьмиугольные/квадратные мозаики
|
[8,4], (*842)
(with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries)
(и подсимметрия [(∞,4,∞,4)] (*4242) )
|
    
=   

=    
=     
|
    
=   
|
    
=   
=    

=     
|
    

=    
|
    

=    
=    
|
    


=    
|
    
|

|
|

|
|

|

|

|
| {8,4}
|
t{8,4}
|
r{8,4}
|
2t{8,4}=t{4,8}
|
2r{8,4}={4,8}
|
rr{8,4}
|
tr{8,4}
|
| Однордные двойственные
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|

|

|

|

|

|

|
| V84
|
V4.16.16
|
V(4.8)2
|
V8.8.8
|
V48
|
V4.4.4.8
|
V4.8.16
|
| Альтернированные
|
[1+,8,4]
(*444)
|
[8+,4]
(8*2)
|
[8,1+,4]
(*4222)
|
[8,4+]
(4*4)
|
[8,4,1+]
(*882)
|
[(8,4,2+)]
(2*42)
|
[8,4]+
(842)
|
    
=    
|
    
=   
|
    
=    
|
    
=    
|
    
=   
|
    
=    
|
    
|

|

|

|

|

|

|

|
| h{8,4}
|
s{8,4}
|
hr{8,4}
|
s{4,8}
|
h{4,8}
|
hrr{8,4}
|
sr{8,4}
|
| Альтернированные двойственные
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|
|

|

|

|

|
|
| V(4.4)4
|
V3.(3.8)2
|
V(4.4.4)2
|
V(3.4)3
|
V88
|
V4.44
|
V3.3.4.3.8
|
| Однородные мозаики (4,4,4)
|
| Симметрия: [(4,4,4)], (*444)
|
[(4,4,4)]+
(444)
|
[(1+,4,4,4)]
(*4242)
|
[(4+,4,4)]
(4*22)
|
   
    
|
   
    
|
   
    
|
   
    
|
   
    
|
   
    
|
   
    
|
   
    
|
   
    
|
   
    
|

|

|

|

|

|

|

|

|

|

|
t0(4,4,4)
h{8,4}
|
t0,1(4,4,4)
h2{8,4}
|
t1(4,4,4)
{4,8}1/2
|
t1,2(4,4,4)
h2{8,4}
|
t2(4,4,4)
h{8,4}
|
t0,2(4,4,4)
r{4,8}1/2
|
t0,1,2(4,4,4)
t{4,8}1/2
|
s(4,4,4)
s{4,8}1/2
|
h(4,4,4)
h{4,8}1/2
|
hr(4,4,4)
hr{4,8}1/2
|
| Однородные двойственные
|

|

|

|

|

|

|

|

|

|

|
| V(4.4)4
|
V4.8.4.8
|
V(4.4)4
|
V4.8.4.8
|
V(4.4)4
|
V4.8.4.8
|
V8.8.8
|
V3.4.3.4.3.4
|
V88
|
V(4,4)3
|
См. также
Примечания
Литература
Ссылки
|















































































