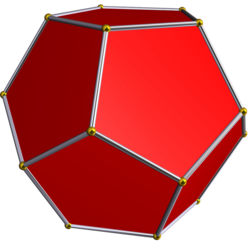
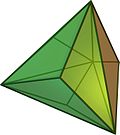
Двенадцатигранники

Двенадцатигра́нник — многогранник с двенадцатью гранями.

Существует несколько объёмных фигур с двенадцатью гранями.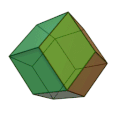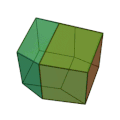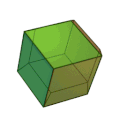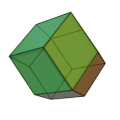

С древнейших времён известна фигура, у которой 12 граней, это правильный додекаэдр. Такой додекаэдр — одно из пяти платоновых тел и обладает симметрией вращения пятого порядка. Однако, у этого во многих отношениях идеального многогранника есть недостаток. Дело в том, что правильными пятиугольниками нельзя без зазоров покрыть плоскость. Также додекаэдрами невозможно плотно заполнить пространство. Из этого следует невозможность существования кристаллов с осями симметрии пятого порядка и невозможность существования кристаллов в форме платонова додекаэдра. Однако, известны вирусы и белки́ в форме такого додекаэдра, с осями симметрии пятого порядка. Предполагают, что они приобрели такую форму во избежание кристаллизации.

Три из четырех тел Кеплера-Пуансо также являются правильными додекаэдрами.

Визуально очень похож на платоново тело, но имеет совсем другую симметрию — центральный вид симметрии кубической сингонии. Грани — неправильные пятиугольники, симметричные относительно плоскости, проходящей через центр фигуры. Пентагондодекаэдр это одна из простых форм кристаллов. Огранка кристаллов пентагондодекаэдром характерна, например, для пирита.

Фигура, огранённая равными ромбами и являющаяся двойственным кубооктаэдру многогранником.

Между пентагондодекаэдром и ромбододекаэдром существует непосредственная связь. Пентагондодекаэдр получается из ромбододекаэдра, если отклонить грань ромбододекаэдра в сторону вершины. В этом смысле, пентагондодекаэдр является переходной формой между кубом и ромбододекаэдром.

• 
  индекс грани {10,9,0}
• 
  индекс грани {2,1,0}
• 
  индекс грани {7,1,0}

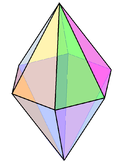
Фигура, получающаяся при соединении двух одинаковых правильных шестиугольных пирамид через их основания.

• 
  Гексагональная бипирамида

В кристаллографии два важных додекаэдра встечаются в виде кристаллических форм в некотором классе симметрий кубической сингонии, которая топологически эквивалентна правильному додекаэдру, но менее симметрична — пиритоэдр с пиритоэдральной симметрей и тетартоид с тетраэдральной симметрией.

Пиритоэдр (или пятиугольный додекаэдр) — это додекаэдр с пиритоэдральной симметрией T_h. Подобно правильному додекаэдру он имеет двенадцать одинаковых пятиугольных граней при трёх сходящихся в каждой из 20 вершин гранях. Однако не требуется, чтобы пятиугольники были правильными. 30 рёбер многогранника делятся на два множества, содержащих 24 и 6 рёбер с одинаковыми длинами. Единственные оси вращения — три попарно перпендикулярные второго порядка и четыре оси третьего порядка^[1]. Хотя правильный додекаидр не встречается в кристаллах, пиритоэдр встречается в кристаллах пирита^[1] и это может послужить источником вдохновения для открытия формы правильного многогранника^[2]. Настоящий правильный додекаэдр может оказаться для квазикристаллов (таких как Квазикристалл сплава гольмия, магния и цинка^[англ.]) с икосаэдральной симметрией, котоая включает истинные оси вращения пятого порядка^[3].

Название Кристалл пирита пришло из одного из двух гибитусов (обликов) кристаллов, образованных пиритом (другой - куб). В пироэдральном пирите грани имеют индекс Миллера (210), что означает, что двугранный угол равен 2·arctan(2) ≈ 126.87° и каждая пятиугольная грань имеет один угол примерно 121.6° между двумя углами примерно в 106.6°, а противоположные два угла равны примерно 102.6°. Следующие формулы показывают размеры грание в идеальном кристалле (который редко встречается в природе).

${\displaystyle {\text{Высота}}={\frac {\sqrt {5}}{2}}\cdot {\text{Длинная сторона}}}$

${\displaystyle {\text{Ширина}}={\frac {4}{3}}\cdot {\text{Длинная сторона}}}$

${\displaystyle {\text{Короткие стороны}}={\sqrt {\frac {7}{12}}}\cdot {\text{Длинная сторона}}}$

Природный пирит (справа - с указанием величины углов на грани)

Восемь вершин куба имеют координаты (±1, ±1, ±1).

Координаты 12 других вершин (0, ±(1 + h), ±(1 − h²)), (±(1 + h), ±(1 − h²), 0) и (±(1 − h²), 0, ±(1 + h)).

Здесь h — высота клиновидной «крыши» над гранью губа со стороной длины 2.

Важный случай — h = 1/2 (четверть длины куба) для идеального природного пирита (also the pyritohedron in the Структура Уэйра - Фелана^[англ.]).

Другой важный случай — h = 1/φ = 0.618... для правильного додекаэдра. Смотрите раздел Геометрическая свобода для других вариантов.

Два пироэдра с обмененными ненулевыми координатами находятся в двойственных позиция друг друга как додекаэдры в соединении двух додекаэдров^[англ.].

Ортогональные проекции пиритоэдра с h = 1/2

Высоты 1/2 и 1/φ

Анимация
Соты из чередующихся выпуклых и вогнутых перитоэдров с высотой между ±1/φ	Высоты между 0 (куб) и 1 (ромбододекаэдр)

Пироэдр имеет геометрическю свободу с предельными случаями - кубическая выпуклая оболочка с коллинеарными рёбрами в качестве одного предела и ромбододекаэдр в качестве другого предела, когда 6 рёбер вырождаются до нулевой длины. Правильный додекаэдр представляет специальный промежуточный случай, когда все рёбра и углы равны.

Можно обойти эти предельные случаи, создавая вогнутые или невыпуклые перитоэдры. Эндододекаэдр является вогнутым и равносторонним, вместе с выпуклым правильным додекаэдром он может заполнять пространство. Продолжая в том же направлении мы проходим вырожденный случай, когда двенадцать вершин оказываются в центре, и получаем правильный большой звёздчатый додекаэдр, когда все рёбра и углы снова становятся равными, а грани превращаются в правильные пентаграммы. В другую сторну проходим ромбододекаэдр и получаем невыпуклый равносторонний додекаэдр с похожими на рыбки самопересекающимися равносторонними пятиугольными гранями.

Специальные случаи пиритоэдра
Версии с равными по абсолюьной величине и противоположными знаками вместе образуют соты. (Сравните эту анимацию.) Показанное отношение — отношение длин, а именно длин из множества 24 рёбер к длинам рёбер из множества 6 рёбер.
Отношение	1 : 1	0 : 1	1 : 1	2 : 1	1 : 1	0 : 1	1 : 1
h	−√5 + 1/2	−1	−√5 + 1/2	0	√5 − 1/2	1	√5 + 1/2
	−1.618...		−0.618...		0.618...		1.618...
Изображение	Правильная звезда, большой звёздчатый додекаэдр, с гранями в виде пентаграмм	Вырожденный додекаэдр, 12 вершин в центре	Вогнутый равносторонний додекаэдр, называемый эндододекаэдром.	куб может быть разделён в пиритоэдр путём деления пополам всех рёбер и деления граней в чередующихся направлениях.	Правильный додекаэдр является промежуточным случаем с равными длинами рёбер.	Ромбододекаэдр является вырожденным случаем, когда 6 рёбер сокращаются до нулевой длины.	Самопересекающийся равносторонний додекаэдр

Тетартоид (также четырёхугольный пятиугольный додекаэдр, четырёхгранный пятиугольный додекаэдр) — это додекаэдр с хиральной тетраэдральной симметрией (T). Подобно правильному додекаэдру, он имеет двенадцать одинаковых пятиугольных граней, которые по три встречаются в каждой из 20 вершин. Однако пятиугольники не являются правильными и фигура не обладает осями симметрии порядка 5.

Хотя правильный додекаэдр в кристаллах не существует, тетартоидная форма встречается. Название тетартоид происходит от греческого «одна четвёртая», поскольку он имеет четверть полной октаэдральной симметрии и половину пирамидальной^[4] Минерал кобальтит может иметь симметрию этого вида^[5].

Абстракции, имеющие ту же топологию и симметрию, что и тело, могут быть созданы из куба и тетраэдра. В кубе каждая грань делится пополам наклонным ребром. В тетраэдре каждое ребро делится на три части и каждая новая вершина соединяется с центром одной из граней. (В нотации Конвея это гиротетраэдр.)

Ортогональные проекции на 2- и 3-кратные оси

Кубическая и тетраэдральная формы

Связь с диакисдодекаэдром

Тетартоид может быть создан путём удлиннения 12 из 24 граней диакисдодекаэдра[англ.]. (Тетартоид, показанный здесь, сам получен путём увеличения 24 из 48 граней дисдакисдодекаэдра.) Хиральные тетартоиды, основанные на диакисдодекаэдре (в середине) моделях кристаллов[англ.] справа показывает тетартоид, созданный путём удлиннения синих граней диакисдодекаэдра. Поэтому рёбра между синими гранями покрыты красными скелетными рёбрами.

Следующие точки являются вершинами тетартоида с тетраэдральной симметрией:

(a, b, c); (−a, −b, c); (−n/d₁, −n/d₁, n/d₁); (−c, −a, b); (−n/d₂, n/d₂, n/d₂),

при следующих условиях:^[6]

0 ≤ a ≤ b ≤ c,

n = a²c − bc²,

d₁ = a² − ab + b² + ac − 2bc,

d₂ = a² + ab + b² − ac − 2bc,

nd₁d₂ ≠ 0.

Правильный додекаэдр — это тетартоид с большей симметрией, чем требуется. Триакистетраэдр является вырожденным случаем с 12 рёбрами нулевой длины. (В терминах цветов, использованных выше, это означает, белые вершины и зелёные рёбра поглощаются зелёными вершинами.)

Вариации тетартоида от правильного додекаэдра до триакистетраэдра