கோசீக்கெண்ட் (முக்கோணவியல்)

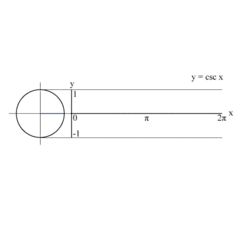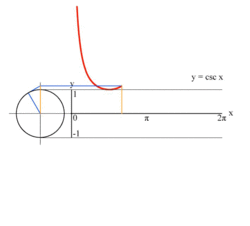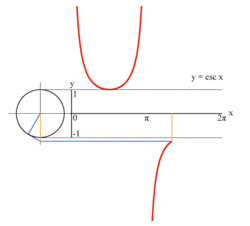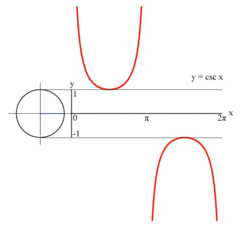
கணிதத்தில் கோசீக்கெண்ட் (cosecant) சார்பு என்பது ஒரு கோணத்தின் சார்பாகும். ஆறு முக்கோணவியல் சார்புகளுள் இதுவும் ஒன்றாகும். இந்த ஆறு சார்புகளில் முதலாவதாக வரிசைப்படுத்தப்படும் சைன் சார்பின் தலைகீழிச் சார்பு அதாவது சைனின் தலைகீழி, கோசீக்கெண்ட் ஆகும்.

ஒரு செங்கோண முக்கோணத்தின் கோணம் A -ன் முக்கோணவியல் சார்புகளை வரையறுக்க அம்முக்கோணத்தின் பக்கங்களைப் பின்வருமாறு அழைக்கலாம்:

• செம்பக்கம் (அல்லது கர்ணம்) (hypotenuse):

செங்கோணத்திற்கு எதிர்ப்பக்கம். இதன் அளவு  h. ஒரு செங்கோண முக்கோணத்தில் செம்பக்கந்தான் மூன்று பக்கங்களிலும் நீளமானது.

• எதிர்ப்பக்கம் (opposite):

நாம் எடுத்துக்கொண்ட கோணம் A -க்கு எதிரில் அமையும் பக்கம். இதன் நீளம்  a.

• அடுத்துள்ள பக்கம் (adjacent):

செங்கோணம் மற்றும் நாம் எடுத்துக்கொண்ட கோணம் இரண்டிற்கும் ( A மற்றும் C) பொதுவான பக்கம். இதன் நீளம்  b.

கோணம் A -ன் கோசீக்கெண்ட்:

csc(A) அல்லது cosec(A)

${\displaystyle \csc A={\frac {1}{\sin A}}={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {h}{a}}.}$

ஒரு செங்கோண முக்கோணம் A கோணத்தைக் கொண்டதாய் அமைந்தால் போதும், அம்முக்கோணத்தின் அளவினை இவ்விகிதம் சார்ந்திருப்பதில்லை. ஏனென்றால் அவ்வாறு அமையும் செங்கோண முக்கோணங்கள் எல்லாம் வடிவொத்த முக்கோணங்களாக அமையும். மேலும் வடிவொத்த முக்கோணங்களின் ஒத்த பக்கங்களின் விகிதங்கள் சமமாக இருக்கும

கொசீக்கெண்ட் சார்பை முடிவிலாத் தொடராக பின்வருமாறு வரையறுக்கலாம்:

${\displaystyle {\begin{aligned}\csc x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x^{-1}+{\frac {1}{6}}x+{\frac {7}{360}}x^{3}+{\frac {31}{15120}}x^{5}+\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}}$

B_n : n -ஆம் பெர்னெளலியின் எண்

${\displaystyle \theta }$ -ன் அனைத்து மதிப்புகளுக்கும் பின்வரும் முற்றொருமைகள் மெய்யாகும்:

• ${\displaystyle \csc \theta ={\frac {1}{\sin \theta }}}$

• ${\displaystyle \csc \theta =\sec \left({\frac {\pi }{2}}-\theta \right)}$

• ${\displaystyle 1+\cot ^{2}\theta =\csc ^{2}\theta .\!}$

• பிற ஐந்து முக்கோணவியல் சார்புகள் வாயிலாக:

${\displaystyle \csc \theta =\!}$

= ${\displaystyle {\frac {1}{\sin \theta }}\!}$

= ${\displaystyle \pm {\frac {1}{\sqrt {1-\cos ^{2}\theta }}}\!}$

= ${\displaystyle \pm {\frac {\sqrt {1+\tan ^{2}\theta }}{\tan \theta }}\!}$

= ${\displaystyle \pm {\frac {\sec \theta }{\sqrt {\sec ^{2}\theta -1}}}\!}$

= ${\displaystyle \pm {\sqrt {1+\cot ^{2}\theta }}\!}$

கோசீக்கெண்ட் சார்பின் நேர்மாறுச் சார்பு:

arccsc அல்லது (csc⁻¹).

${\displaystyle \theta =\operatorname {arccsc} \left({\frac {\text{hypotenuse}}{\text{opposite}}}\right)=\csc ^{-1}\left({\frac {h}{a}}\right).}$

k, ஏதேனும் ஒரு முழு எண் எனில்:

${\displaystyle \csc(y)=x\ \Leftrightarrow \ y=\operatorname {arccsc}(x)+2k\pi {\text{ or }}y=\pi -\operatorname {arccsc}(x)+2k\pi }$