沙普利-福克曼引理

沙普利-福克曼引理是凸幾何（英语：Convex geometry）的一條引理，其於数理经济学有應用。引理描述向量空間子集的閔可夫斯基和有何性質。若干個集合的閔可夫斯基和，即從各集合分別取一個元素相加，組成的集合：例如，將整數${\displaystyle 0}$和${\displaystyle 1}$組成的集合，與自身相加，得到由${\displaystyle 0,\ 1,\ 2}$組成的集合，以符號可寫成：

${\displaystyle \{0,1\}+\{0,1\}=\{0,1,2\}.}$

「許多個集合的閔氏和，是否必定近似凸集？」沙普利-福克曼引理和相關的結果表明，問題的答案為肯定。^[2]集合稱為凸，意思是連接其中任意兩點的线段，必為該集合的子集：舉例，實心圓盤 ${\displaystyle \bullet }$ 為凸集，但圓 ${\displaystyle \circ }$ 則不然，因為連接相異兩點的線段 ${\displaystyle \oslash }$ 並不是圓的子集。沙普利-福克曼引理大致斷言，若求和項的數目超出向量空間的維數，則其閔氏和將近凸。^[1]

沙普利-福克曼引理引入時，是作為證明沙普利-福克曼定理的一步，該定理斷言閔氏和與其凸包的距離不超過某個上界。所謂集合${\displaystyle Q}$的凸包，是包含${\displaystyle Q}$的最小凸集。而當且僅當和為凸時，上述距離為零。定理中，距離的上界取決於維數${\displaystyle D}$及求和項的形狀，但不取決於求和的項數${\displaystyle N}$，而只需${\displaystyle N>D}$。只要其中${\displaystyle D}$個求和項的形狀，就足以確定${\displaystyle N}$個集合的閔可夫斯基平均集

${\displaystyle {\frac {1}{N}}\left(Q_{1}+Q_{2}+\cdots +Q_{N}\right)}$

與其凸包的距離的上界。當${\displaystyle N}$趨向無窮時，該上界遞減至零（需要各求和項的大小一致有界）。^[3]斯塔（Starr）的推论將沙普利-福克曼定理的上界壓得更低，故又稱為沙普利-福克曼-斯塔定理。

劳埃德·沙普利和強·福克曼（英语：Jon Folkman）的引理，最先由經濟學家羅斯·斯塔（英语：Ross Starr）發表，其時斯塔正在肯尼斯·阿罗門下，研究經濟均衡的存在性。^[1]斯塔在論文中，研究凸化（convexified）經濟體，即將非凸集換成其凸包。斯塔證明，凸化之後，有些均衡由原經濟體的「準均衡」（quasi-equilibria）逼近；還證明，每個準均衡都具有真均衡的許多最優性質，而凸經濟體中則必定存在真均衡。斯塔1969年的論文發表後，沙普利-福克曼-斯塔的結果得到廣泛應用，用作證明（凸）經濟理論的若干核心結果，儘管不適用於有非凸部分的大經濟體，但在此等經濟體中，仍是良好的近似。羅歇·蓋內里（英语：Roger Guesnerie）評論：「這些結論的一般形式的推導，是戰後經濟理論的重大成就。」^[4]許多諾貝爾獎得主都曾研究經濟學中的非凸集（英语：Non-convexity (economics)），除了前述的劳埃德·沙普利（2012年獲獎）外，還有：阿羅（1972）、罗伯特·约翰·奥曼（2005）、傑拉德·德布魯（1983）、特亚林·科普曼斯（1975）、保羅·克魯曼（2008）、保羅·薩繆爾森（1970）。至於互補的主題「經濟學中的凸集（英语：Convexity in economics）」，除以上得主著重外，還有里奥尼德·赫维克兹、列昂尼德·维塔利耶维奇·康托罗维奇（1975）、罗伯特·索洛（1987）都著重。

沙普利-福克曼引理在優化論和概率论皆有應用。^[3]優化論中，可以引理解釋，在求多個函数之和的最小值時，為何一些解法可以成功。^[5][6]概率論中，引理適用於證明隨機集（英语：Stochastic geometry）的「大數定律」。此定理先前僅在凸集的情況得證。^[7]

考慮凸的實數區間${\displaystyle [0,1]}$，其包含整數子集${\displaystyle \{0,1\}}$，且是其凸包（添加了兩點所連線段上的所有點）。僅得兩個元素的集合${\displaystyle \{0,1\}}$，複製成三份，並按元素求和，得到

${\displaystyle \{0,1\}+\{0,1\}+\{0,1\}=\{0,1,2,3\}.}$

（此處集合的和，是從各集合分別取一個元素相加，得到的可能結果的集合，稱為閔氏和。）和集的凸包則為區間${\displaystyle [0,3]}$。

區間${\displaystyle [0,3]}$中，每個數${\displaystyle x}$都可以寫成區間${\displaystyle [0,1]}$中某三個實數（允許重複）之和，例如將${\displaystyle x}$等分成三份即可。但使用沙普利-福克曼引理，則有更強的結論：${\displaystyle [0,3]}$的每個數，都可以寫成${\displaystyle \{0,1\}}$中某兩個整數（允許重複），與${\displaystyle [0,1]}$中某一個實數之和。^[8]

凸包${\displaystyle [0,1]}$中的點，到${\displaystyle \{0,1\}}$的距離，至多為${\displaystyle 1/2}$：

${\displaystyle {\frac {1}{2}}=\left|{\frac {1}{2}}-0\right|=\left|{\frac {1}{2}}-1\right|,}$

然而，考慮三個區間${\displaystyle [0,1]}$的閔氏平均

${\displaystyle {\frac {1}{3}}\left(\{0,1\}+\{0,1\}+\{0,1\}\right)=\left\{0,{\frac {1}{3}},{\frac {2}{3}},\ 1\right\},}$

與其凸包${\displaystyle [0,1]}$的距離，僅為${\displaystyle 1/6}$，即未平均前${\displaystyle \{0,1\}}$與${\displaystyle [0,1]}$距離（${\displaystyle 1/2}$）的三分之一。越多個集合相加，其閔氏平均就將凸包填得越滿：由閔氏平均至凸包的最遠距離，隨被加項數增加，而趨向於零。^[8]此為沙普利-福克曼定理的結論。

沙普利-福克曼引理需要用到凸幾何（英语：convex geometry）的若干定義和定理，本節將作簡介。

二維的實向量空間上，有笛卡兒坐標系，將每點視為一對實數，稱為「坐標」，按慣例記為${\displaystyle x,\ y}$。笛卡兒平面上的兩點，可以逐個坐標相加：

${\displaystyle (x_{1},y_{1})+(x_{2},y_{2})=(x_{1}+x_{2},y_{1}+y_{2}).}$

此外，點也可以逐個坐標與實數${\displaystyle \lambda }$相乘：

${\displaystyle \lambda (x,y)=(\lambda x,\lambda y).}$

更一般而言，任何${\displaystyle D}$維（有限維）實向量空間，均可視為${\displaystyle D}$個實數組成的D元組的集合${\displaystyle \{(v_{1},v_{2},\ldots ,v_{D})\}}$，並配備兩種運算：向量加法和標量乘法。有限維實空間的此兩種運算，皆定義成逐個坐標運算，與笛卡兒平面上的運算類似。^[9]

凸集${\displaystyle Q}$中，連接任意兩點的線段仍是${\displaystyle Q}$的子集。

非凸集${\displaystyle Q}$中，連接某兩點的線段上，有一點不再是${\displaystyle Q}$的元素。

用線段可以檢驗某集合是否凸集。

實向量空間中，非空子集${\displaystyle Q}$稱為凸集，意思是，對於${\displaystyle Q}$的任意兩個點，連接兩點成一線段，其上的所有點仍在${\displaystyle Q}$中。例如，實心圓盤 ${\displaystyle \bullet }$ 為凸，但圓 ${\displaystyle \circ }$ 則不然，因為連接相異兩點的線段 ${\displaystyle \oslash }$ 並不是圓的子集。三個整數的集合${\displaystyle \{0,1,2\}}$非凸，但其為區間${\displaystyle [0,2]}$的子集，而該區間為凸。又例如，實心立方體為凸，然而任何空心或凹陷的圖形，如彎月形（英语：Crescent），則非凸。空集也是凸集，視乎作者偏好，這可能是專門的定義^[10]，也可能是因為要滿足的條件是空真命題（英语：Vacuous truth）。

更嚴謹而言，集合${\displaystyle Q}$稱為凸，意思是，對${\displaystyle Q}$中任意兩點${\displaystyle v_{0},v_{1}}$，和單位區間${\displaystyle [0,1]}$中的任意實數${\displaystyle \lambda }$，點

${\displaystyle (1-\lambda )v_{0}+\lambda v_{1}}$

仍是${\displaystyle Q}$的元素。

由數學歸納法，集合${\displaystyle Q}$為凸，當且僅當其任意多個元素的凸組合仍在${\displaystyle Q}$中。所謂向量空間子集${\displaystyle \{v_{0},v_{1},\ldots ,v_{D}\}}$的凸組合，是其元素的任意加權平均${\displaystyle \lambda _{0}v_{0}+\lambda _{1}v_{1}+\cdots +\lambda _{D}v_{D}}$，而各${\displaystyle \lambda _{i}}$可以是總和為${\displaystyle 1}$的任意非負實數，即只需${\displaystyle \lambda _{0}+\lambda _{1}+\cdots +\lambda _{D}=1}$。^[11]

凸集的定義推出，兩個凸集的交集仍是凸集。更甚者，任意一族凸集的交也是凸集。作為特例，若取兩個不交的凸集，則其交集為空集，故應當稱空集為凸。^[10]

對於實向量空間的每個子集${\displaystyle Q}$，其凸包${\displaystyle \mathrm {Conv} (Q)}$是包含${\displaystyle Q}$的最小凸集。所以，${\displaystyle \mathrm {Conv} (Q)}$是所有覆蓋${\displaystyle Q}$的凸集的交。等價地，可以將${\displaystyle \mathrm {Conv} (Q)}$定義成${\displaystyle Q}$的點的所有凸组合的集合。^[12]作為例子，整數集合${\displaystyle \{0,1\}}$的凸包，是實數閉區間${\displaystyle [0,1]}$，其兩端為原有的整數${\displaystyle 0,1}$。^[8]单位圆的凸包則是閉单位圆盘，其包含單位圓。

在任何向量空間（或有定義加法的代數結構）${\displaystyle X}$中，兩個非空子集${\displaystyle A,B\subseteq X}$的閔可夫斯基和，定義為其元素之和的集合，即 ${\displaystyle A+B:=\{x+y\mid x\in A,~y\in B\}}$（參見^[13])。例如：

${\displaystyle \{0,1\}+\{0,1\}=\{0+0,0+1,1+0,1+1\}=\{0,1,2\}.}$

此運算定義在非空子集族上，且滿足結合律和交換律。既然有結合律和交換律，就可以遞歸定義多個被加項的運算結果${\displaystyle \sum _{n=1}^{N}Q_{n}=Q_{1}+Q_{2}+\cdots +Q_{N}}$。由數學歸納法，可見^[14]

${\displaystyle \sum _{n=1}^{N}Q_{n}=\left\{\left.\sum _{n=1}^{N}q_{n}\right|q_{n}\in Q_{n},~1\leq n\leq N\right\}.}$

閔可夫斯基和與凸包運算可以交換。具體而言，對實向量空間${\displaystyle X}$的任意子集${\displaystyle A,B\subseteq X}$，其閔氏和的凸包等於其凸包的閔氏和。換言之，

${\displaystyle \mathrm {Conv} (A+B)=\mathrm {Conv} (A)+\mathrm {Conv} (B).}$

故由數學歸納法得

${\displaystyle \mathrm {Conv} (\sum _{n=1}^{N}Q_{n})=\sum _{n=1}^{N}\mathrm {Conv} (Q_{n})}$

對任意${\displaystyle N\in \mathbb {N} }$和非空子集${\displaystyle Q_{n}\subseteq X}$（${\displaystyle 1\leq n\leq N}$）成立。^[15][16]

由前一段的恆等式，對和的凸包中的每點${\displaystyle x\in \mathrm {Conv} \left(\sum _{n=1}^{N}Q_{n}\right)}$，都存在各凸包的${\displaystyle q_{n}(x)\in \mathrm {Conv} (Q_{n})}$（${\displaystyle n}$取遍${\displaystyle 1}$至${\displaystyle N}$），使得${\displaystyle \sum _{n=1}^{N}q_{n}(x)=x}$。各點${\displaystyle q_{n}(x)}$的位置取決於${\displaystyle x}$。

有了以上背景，沙普利-福克曼引理斷言，${\displaystyle x}$的表示法

${\displaystyle x=\sum _{n=1}^{N}q_{n}(x)}$

中，僅需要不多於${\displaystyle D}$個被加項${\displaystyle q_{n}(x)}$取自凸包，而其他被加項，則只需取自原來的集合${\displaystyle Q_{n}}$。以符號復述，即有以上方法表示${\displaystyle x}$，且滿足${\displaystyle |\{l\leq n\leq N\mid q_{n}(x)\in \mathrm {Conv} (Q_{n})\setminus Q_{n}\}|\leq D}$。不妨將下標重新排序，然後就有

${\displaystyle x=\sum _{n=1}^{D}q_{n}(x)+\sum _{n=D+1}^{N}q_{n}(x)}$

其中對${\displaystyle 1\leq n\leq D}$，有${\displaystyle q_{n}\in \mathrm {Conv} (Q_{n})}$，而對${\displaystyle D+1\leq n\leq N}$，則有${\displaystyle q_{n}\in Q_{n}}$。注意，倘若重排，則排序的方式也取決於點${\displaystyle x}$。^[17]再精簡，沙普利-福克曼引理可以寫成

${\displaystyle \mathrm {Conv} (\sum _{n=1}^{N}Q_{n})\subseteq \bigcup _{I\subseteq \{1,2,\ldots N\}:~|I|=D}\sum _{n\in I}\mathrm {Conv} (Q_{n})+\sum _{n\notin I}Q_{n}.}$

舉例，集合${\displaystyle [0,2]=[0,1]+[0,1]=\mathrm {Conv} (\{0,1\})+\mathrm {Conv} (\{0,1\})}$中的每個點，根據引理，必定可以寫成${\displaystyle \{0,1\}}$的某個元素，與${\displaystyle [0,1]}$的某個元素之和。^[8]

反之，沙普利-福克曼引理刻劃了有限維實向量空間的維數。具體而言，若某向量空間，對於某個自然數${\displaystyle D}$滿足引理的結論，但對小於${\displaystyle D}$的數不滿足，則其維數恰好為${\displaystyle D}$。^[18]引理僅對有限維向量空間成立。^[19]

沙普利與福克曼運用其引理，證明沙普利-福克曼定理，給出集合的閔氏和與其凸包（稱為凸化（convexified）和）的距離上界。定理的敍述如下：

凸化和${\displaystyle \mathrm {Conv} \left(\sum Q_{n}\right)}$的任一點，到（未凸化）和集${\displaystyle \sum Q_{n}}$的歐氏距離平方，不超過各集合${\displaystyle Q_{n}}$的外接半徑中，最大${\displaystyle D}$個的平方和。(所謂外接半徑，定義為包圍該集合的最小球面的半徑。）^[20]此上界與求和項數${\displaystyle N}$無關（但要求${\displaystyle N>D}$，且集合不能越來越大）。^[21]

上述定理給出閔氏和及其凸包之間距離的上界。當且僅當閔氏和為凸集時，此距離為零。該上界取決於維數${\displaystyle D}$及各被加項的形狀，但只要${\displaystyle N>D}$，就不取決於項數${\displaystyle N}$。^[3]

通常，外接半徑會大於內半徑，而無論如何，外接半徑總不能小於內半徑。集合${\displaystyle Q_{n}}$的內半徑定義為：^[22]

最小的正實數${\displaystyle r}$，滿足：若${\displaystyle q}$在${\displaystyle Q_{n}}$凸包中，則${\displaystyle q}$在${\displaystyle Q_{n}}$若干點的凸包中，而該些點皆在同一個半徑為${\displaystyle r}$的球內。

斯塔將沙普利-福克曼定理中的外接半徑換成內半徑，從而壓低沙普利-福克曼定理的上界：

沙普利-福克曼定理的斯塔推論：

凸化和${\displaystyle \mathrm {Conv} \left(\sum Q_{n}\right)}$的任一點，到（未凸化）和集${\displaystyle \sum Q_{n}}$的歐氏距離平方，不超過各集合${\displaystyle Q_{n}}$的內半徑中，最大${\displaystyle D}$個的平方和。^[22][23]

斯塔的推論確定，${\displaystyle N}$個集合的閔氏和與其凸包之間，歐氏距離的上界。此距離可以衡量閔氏和非凸的程度，故為簡單起見，下文稱為非凸度。於是，斯塔對非凸度的上界，僅取決於${\displaystyle D}$個最大內半徑之值，但不取決於求和的項數${\displaystyle N}$（假設${\displaystyle N>D}$）。

例如，非凸集${\displaystyle \{0,1,2\}}$的非凸度為${\displaystyle 1/2}$，因為與其凸包（區間${\displaystyle [0,2]}$）的距離為

${\displaystyle {\frac {1}{2}}=\left|1-{\frac {1}{2}}\right|=\left|0-{\frac {1}{2}}\right|=\left|2-{\frac {3}{2}}\right|=\left|1-{\frac {3}{2}}\right|.}$

所以，既然${\displaystyle \sum Q_{n}}$的非凸度有不取決於項數${\displaystyle N}$的上界，就知平均集

${\displaystyle {\frac {1}{N}}\left(\sum Q_{n}\right)}$

非凸度上界，會隨${\displaystyle N}$增加而遞減。例如，平均集

${\displaystyle {\frac {1}{2}}\left(\{0,1\}+\{0,1\}\right)=\{0,\ 1/2,\ 1\}}$

和其凸包${\displaystyle [0,1]}$的距離僅為${\displaystyle 1/4}$，等於被加項${\displaystyle \{0,1\}}$與其凸包${\displaystyle [0,1]}$的距離（${\displaystyle 1/2}$）之半。僅要最大${\displaystyle D}$個求和項的形狀，已足以計算和集與凸包的距離的上界，故除以${\displaystyle N}$後，平均集與凸包的距離，在${\displaystyle N}$趨向無窮時，會遞減至零（對均勻有界的求和項成立，即各個求和項的大小需有同一個上界）。^[3]若使用斯塔的上界，則前一句結論的條件可以放寬，只需各求和項的內半徑有同一個上界。^[3]

沙普利-福克曼引理的原證明，僅確定存在該種表示法，而無說明如何構造。阿羅與哈恩^[24]、蓋士利（英语：J. W. S. Cassels）^[25]、斯奈德（Schneider）^[26]和其他人都曾給出類似的證明。阿特斯泰因（Artstein）擴展了埃科蘭德（英语：Ivar Ekeland）的簡潔抽象證明。^[27][28]也有未經出版的另證。^[2][29]1981年，斯塔發表一種疊代法，可以計算給定點的表示法，然而，此計算方法給出的上界，較非構造性證明的上界差。^[30]博赛卡斯的書有講述有限維空間沙普利-福克曼引理的初等證明，^[31]並將引理應用於估計可分優化（separable optimization）問題與零和賽局的對偶間隙。

有沙普利-福克曼引理，學者就得將有關凸集閔氏和的結果，套用到（無需凸的）一般集合之和。此種和見於經濟學、最优化理論、概率論。此三領域的應用中，非凸性起到重要作用。

經濟學中，消費者對每一「籃子」商品（basket，即商品的組合）有其偏好程度。每籃子可用一個非負向量表示，其坐標為籃中各商品的量。所有籃子組成的集合中，每個消費者有自己的一族无差异曲线，滿足：在同一條曲線上的各籃子，對該消費者是等價的，即消費者並不覺該曲線上有籃子勝於另一個籃子。每籃子恰好處於一條無差異曲線上。消費者相對於一條無差異曲線的偏好集，定義為該無差異曲線與其更偏好的區域的並集。稱消費者的偏好為凸，意思是其所有偏好集皆為凸。^[32]

如圖所示，消費者認為的最優籃子，是在預算線支撐某個偏好集時取到，因為此時，所選的籃子是整條預算線上，達到最高的無差異曲線的一點。所謂預算線，是由商品的價格向量與消費者的收入計算得出的限制，消費者無足夠收入購買高於此線的籃子。所以，最優籃子的集合是各價格的函數，稱為消費者的需求。若偏好集為凸，則不論價格為何，消費者認為的最優籃子總是組成凸集，例如可能是單元集，或是一條線段。^[33]

然而，若有偏好集非凸，則某些價格確定的預算線，可能在兩個分開的最優籃子支撐該偏好集。例如，可以設想，動物園購買獅子或鷹的價錢一樣，且其預算恰好夠買一隻獅子或一隻鷹。此外，假設園主亦認為兩隻動物價值相同，則動物園有可能買獅子，也可能買鷹，但當然不可能買半隻獅子加半隻鷹（狮鹫）。所以，園主的偏好非凸：買兩隻動物中的任一隻，勝於兩者的嚴格凸組合。^[34]

若消費者有非凸偏好集，則對於某些價格，需求不連通。不連通的需求，會導致消費者的行為出現不連續的間斷。引述哈羅德·霍特林的話（宜配合所附動圖理解）：

若考慮波浪形的無差異曲線，即在某些區域向原點凸，而在其他區域向原點凹，則我等被迫推論，僅有向原點凸的部分需要理會，因為幾乎不可能觀測到其他部分。要偵測該些部分，唯一方法是，觀察價格之比率變化時，需求的不連續變化。此變化的效果是，當直線旋轉時，切點會突然躍過某凹陷。雖然此種不連續的表現，揭示有凹陷，但卻不可能量度缺口的深度。倘若無差異曲線，或其高維推廣，有凹陷部分，則定必因永遠無法測量，而不為人知。^[35]

瓦爾特·迪韋爾特（英语：Walter Erwin Diewert）^[36]書中，稱赫爾曼·沃爾德（英语：Herman Wold）^[37]有強調研究非凸偏好的困難，也引述保羅·薩繆爾森稱凹陷處「被永恆的黑暗遮蔽」^[38]。

儘管有上述困難，《政治經濟期刊（英语：Journal of Political Economy）》（JPE）在1959年至1961年間，刊登一系列的論文，解明非凸偏好。投稿人包括：法雷爾（Farrell）^[39]、巴托爾（英语：Francis M. Bator）^[40]、科普曼斯^[41]、羅森博格（Rothenberg）^[42]。其中，羅森博格討論非凸集和的近似凸性。^[43]該些JPE論文，促使劳埃德·沙普利和马丁·舒比克也合著論文，研究凸化的消費者偏好，並引入「近似均衡」（approximate equilibrium）的概念。^[44]JPE論文和沙普利-舒比克論文又啟發了罗伯特·奥曼提出另一個概念，稱為「準均衡」（quasi-equilibrium）。^[45][46]

肯尼斯·阿罗收集前人研究經濟學中的非凸集（英语：Non-convexity (economics)）的文獻，列成表，並加入註解，交給羅斯·斯塔（英语：Ross Starr）。斯塔當時仍是本科生，但已在修讀阿羅開設的高等數理經濟學（研究生）課程。^[47]斯塔在學期論文中，考慮將非凸偏好換成其凸包所得的假想經濟體，研究其一般均衡。凸化經濟體中，在每個價位，總需求皆是各消費者需求的凸包之和。斯塔的想法吸引數學家劳埃德·沙普利和強·福克曼（英语：Jon Folkman）參與，兩人「在私人通信中」證明現以兩人命名的引理和定理，到1969年，斯塔才於論文報告此事。^[1]

斯塔1969年的論文中，應用沙普利-福克曼-斯塔定理，證明「凸化」經濟體有一些一般均衡，只要參與者足夠多，能以原經濟體的「準均衡」近似。具體而言，斯塔證明，至少存在一個價格向量為${\displaystyle p_{\mathrm {opt} }}$的準均衡，滿足下列條件：

• 對每個準均衡${\displaystyle p_{\mathrm {opt} }}$，所有消費者都可以選到其最優的籃子（在預算限制內，且最偏好）。
• 在該價格${\displaystyle p_{\mathrm {opt} }}$，凸化經濟體中，每種商品的市場皆均衡，即供給等於需求。
• 每個準均衡的價格，皆「幾乎出清」原經濟體的市場：凸化經濟體均衡組成的集合，與原經濟體的準均衡集合，兩者的距離有上界。此結論是根據沙普利-福克曼定理的斯塔推論得到。^[48]

斯塔確立以下結論：

「總體中，［取各消費及生產集的凸包］所得的假想經濟體的分配，與真實經濟體的某個分配，兩者的差異，有不取決於參與者數目的上界。因此，當參與者數目趨向無窮時，平均參與者感受到，與擬作行動的偏差，近乎可以忽略不計。」^[49]

斯塔1969年論文發表後，沙普利-福克曼-斯塔的結論，在經濟理論獲廣泛應用。羅歇·蓋內里（英语：Roger Guesnerie）如此總結該結論對經濟學的意義：「假設凸性，所得的若干重要結果，在不具凸性的情況下，仍（近似）適用。例如，若經濟體具有大消費側，則偏好的非凸性不影響適用標準結果」^[50]，還稱「這些結論的一般形式的推導，是戰後經濟理論的重大成就。」^[4]許多諾貝爾獎得主都曾研究經濟學中的非凸集（英语：Non-convexity (economics)），除了前述的劳埃德·沙普利（2012年獲獎）外，還有：阿羅（1972）、罗伯特·约翰·奥曼（2005）、傑拉德·德布魯（1983）、特亚林·科普曼斯（1975）、保羅·克魯曼（2008）、保羅·薩繆爾森（1970）。至於互補的主題「經濟學中的凸集（英语：Convexity in economics）」，除以上得主著重外，還有里奥尼德·赫维克兹、列昂尼德·维塔利耶维奇·康托罗维奇（1975）、罗伯特·索洛（1987）都著重。^[51]

沙普利-福克曼-斯塔的結論，在經濟學各分支的文獻都經常出現，包括微观经济学^[52]、一般均衡理論^[53][54]、公共經濟學^[55]（包括市场失灵）^[56]、博弈论^[57]、数理经济学^[58]、經濟學中的应用数学^[59][60]。沙普利-福克曼-斯塔的結論，也使經濟學更多使用測度論和积分理論。^[61]

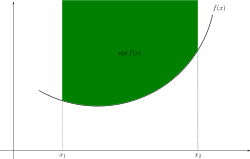
沙普利-福克曼引理可以解釋，為何大規模的最小化問題，即使非凸，仍可用迭代法近似求解（僅對於凸問題，有證明疊代法收斂到最優解）。沙普利-福克曼引理，促使學者將凸優化方法，用於優化多個（無需凸的）函數之和。^[62]

非线性规划依賴下列有關函數的若干定義：

• 函數${\displaystyle f}$（定義在集合${\displaystyle D}$上）的圖像，是所有參數${\displaystyle x}$與相應取值${\displaystyle f(x)}$組成的二元組的集合：

${\displaystyle \mathrm {Graph} (f)=\{(x,f(x)):x\in D\}.}$

• 實值函數（英语：Real-valued function）${\displaystyle f}$的蓋圖（英语：Epigraph (mathematics)）是圖像上方的點的集合：

${\displaystyle \mathrm {Epi} (f)=\{(x,u):f(x)\leq u\}.}$

• 實值函數稱為凸函数，意思是其蓋圖為凸集。^[63]

舉例，二次函数${\displaystyle f:x\mapsto x^{2}}$為凸，而绝对值函數${\displaystyle g:x\mapsto |x|}$亦然，但正弦函數${\displaystyle \sin }$（如圖）則不然，因為在區間${\displaystyle (0,\pi )}$的蓋圖非凸（而有向上的凹陷）。

許多優化問題中，目標函數${\displaystyle f}$可分離變數（可分），即${\displaystyle f}$是多個函數之和，而各個函數的參數不同，如：

${\displaystyle f({\boldsymbol {x}})=f(x_{1},x_{2},\ldots ,x_{n})=\sum _{n}f_{n}(x_{n}).}$

又例如，线性规划問題就可分離變數。考慮一個可分問題，及一個最優解

${\displaystyle {\boldsymbol {x}}_{\mathrm {min} }=(x_{1},x_{2},\ldots ,x_{n})_{\mathrm {min} },}$

在該點取到最小值${\displaystyle f({\boldsymbol {x}}_{\mathrm {min} })}$。對此可分問題，同時考慮其「凸化問題」的最優解，即將每個求和項${\displaystyle f_{n}}$的圖像換成其凸包。此種最優解，會是凸化問題的某點列${\displaystyle ({\boldsymbol {x}}_{j},f({\boldsymbol {x}}_{j}))_{j=1}^{\infty }}$的極限，其中

${\displaystyle ({\boldsymbol {x}}_{j},f({\boldsymbol {x}}_{j}))\in \sum _{n=1}^{N}\mathrm {Conv} (\mathrm {Graph} (f_{n})).}$^[5][64]

當然，因為此點是${\displaystyle N}$個圖像凸包的點之和，由沙普利-福克曼引理，就可以寫成原圖像的點與少數圖像凸包的點之和。

以上分析，1974年由埃科蘭德（英语：Ivar Ekeland）發表，以解釋為何可分問題有許多項時，即使各項非凸，總問題仍看似凸。對非線性最小值問題而言，對偶問題的解，不一定就是原問題的解（但若已知原問題為凸，且滿足特定条件，則兩者的的最優解相等），但是，1973年，青年數學家克勞德·勒馬雷沙爾（英语：Claude Lemaréchal）詫異，對已知非凸的問題使用凸問題的方法，竟然也成功。勒馬雷沙爾的問題，正是上段加性可分離變數的形式，而每個和項皆非凸函數，但對偶問題的解，仍近似原問題的最優解。^[65][5][66]埃科蘭德的分析說明，「大而可分」的最小值問題，即使各和項有凹陷，仍可運用凸優化的方法。埃科蘭德及其後的作者主張，因為變數可以加性分離，所得的總問題近似凸。該等著作以沙普利-福克曼引理為關鍵一步。^[5][66][67]沙普利-福克曼引理促使學者將凸優化方法，應用到目標函數為多個函數之和的情況。^{[5][6][59][62]}

凸集常與概率论一同研究。卡拉西奧多里定理（英语：Carathéodory's theorem (convex hull)）說明，${\displaystyle d}$維空間的（非空）子集${\displaystyle Q}$凸包中的點，是取值於${\displaystyle Q}$的簡單隨機向量（英语：Multivariate random variable）的期望值，而所謂簡單，意思是僅在不多於${\displaystyle d+1}$個點處有非零概率。所以，對非空集${\displaystyle Q}$，取值自${\displaystyle Q}$的簡單隨機向量組成的集合，等於${\displaystyle Q}$的凸包。由此便可在概率論中，套用沙普利-福克曼-斯塔的結果。^[68]反之，藉期望值與凸包之間的聯繫，概率論亦能用作研究凸集，尤其可用作分析沙普利-福克曼-斯塔的結果。^[69]沙普利-福克曼-斯塔的結果，廣泛用於隨機集的概率論（英语：Stochastic geometry）^[70]，例如證明隨機集的大數定律^[7][71]、中央極限定理^[71][72]、大離差原理（英语：Large deviations theory）^[73]。要證明前列概率極限定理，可以使用沙普利-福克曼-斯塔的結果，來避免假設隨機集為凸。

概率测度是有限的测度，而沙普利-福克曼引理還可以應用到非概率的測度論，如体积或向量测度的理論。沙普利-福克曼引理可以加強布倫-閔可夫斯基不等式（英语：Brunn–Minkowski theorem）。該不等式斷言，閔氏和的體積，相較於各和項的體積不能太大，即閔氏和的體積有上界，以各和項的體積的表示。^[74]歐氏空間子集的體積，此處定義為其勒贝格测度。

高等測度論中，沙普利-福克曼引理適用於證明李亞普諾夫定理，即向量测度的值域為凸。^[75]值域（或像集）是函數所有可能取值的集合，而向量測度則將測度推廣到允許取向量值。例如，若某测度空間有兩種概率测度${\displaystyle p_{1}}$和${\displaystyle p_{2}}$，則可定義一個向量測度${\displaystyle (p_{1},p_{2})}$，是對每個事件${\displaystyle \omega }$，將其兩個概率結合為一個二元組，即

${\displaystyle (p_{1},p_{2})(\omega )=(p_{1}(\omega ),p_{2}(\omega )).}$

李亞普諾夫定理在經濟學^[45][76]、(砰砰)控制論、統計理論（英语：Statistical theory）皆有應用。^[77]李亞普諾夫定理是沙普利-福克曼引理的連續版^[3]，而沙普利-福克曼引理是李亞普諾夫定理的離散類比。^[78]

• Anderson, Robert M. Nonconvex preferences and approximate equilibria [非凸偏好與近似均衡] (PDF). Economics 201B: Economic Theory (Handouts) [經濟學201B: 經濟理論（課堂講義）]. Robert M. Anderson's homepage (Berkeley, Calif.). 14 March 2005: 1–5 [1 January 2011]. （原始内容存档 (PDF)于2012-03-10） （英语）. 
• Arrow, Kenneth J.; Hahn, Frank H. General competitive analysis [一般競爭分析]. Advanced Textbooks in Economics 12 San Francisco, CA: Holden-Day, Inc. Mathematical Economics Texts 6之重印版. Amsterdam: North-Holland. 1980 [1971]. ISBN 0-444-85497-5. MR 0439057 （英语）. 
• Artstein, Zvi. Discrete and continuous bang-bang and facial spaces, or: Look for the extreme points [離散與連續砰砰及面空間，又或：找極值點]. SIAM Review. 1980, 22 (2): 172–185. JSTOR 2029960. MR 0564562. doi:10.1137/1022026 （英语）. 
• Carter, Michael. Foundations of mathematical economics [數理經濟學基礎]. Cambridge, Mass.: MIT Press. 2001: xx+649. ISBN 0-262-53192-5. MR 1865841. (作者網站有習題題解). （原始内容存档于15 September 2006） （英语）. 
• Diewert, W. E. 12 Duality approaches to microeconomic theory [第12章：微觀經濟學的對偶進路]. Arrow, Kenneth Joseph; Intriligator, Michael D (编). Handbook of mathematical economics, Volume II [數理經濟學手冊・卷二]. Handbooks in Economics 1. Amsterdam: North-Holland Publishing Co. 1982: 535–599 [2021-08-31]. ISBN 978-0-444-86127-6. MR 0648778. doi:10.1016/S1573-4382(82)02007-4. （原始内容存档于2012-12-10） （英语）. 
• Ekeland, Ivar. Appendix I: An a priori estimate in convex programming [附錄一：凸規劃的先驗估計]. Ekeland, Ivar; Temam, Roger (编). Convex analysis and variational problems [凸分析與變分問題]. Classics in Applied Mathematics 28 Corrected reprinting of the North-Holland. Philadelphia: Society for Industrial and Applied Mathematics (SIAM). 1999: 357–373 [1976]. ISBN 0-89871-450-8. MR 1727362 （英语）. 
• Green, Jerry; Heller, Walter P. 1 Mathematical analysis and convexity with applications to economics [第1章：數學分析與凸性，及在經濟學之應用]. Arrow, Kenneth Joseph; Intriligator, Michael D (编). Handbook of mathematical economics, Volume I. Handbooks in Economics 1. Amsterdam: North-Holland Publishing Co. 1981: 15–52. ISBN 0-444-86126-2. MR 0634800. doi:10.1016/S1573-4382(81)01005-9 （英语）. 
• Guesnerie, Roger. First-best allocation of resources with nonconvexities in production [生產非凸的資源之最優分配]. Cornet, Bernard; Tulkens, Henry (编). Contributions to Operations Research and Economics: The twentieth anniversary of CORE (Papers from the symposium held in Louvain-la-Neuve, January 1987) [運籌學與經濟學投稿：二十周年（[[新魯汶]]1987年舉辦討論會的論文集）]. Cambridge, Mass.: MIT Press. 1989: 99–143. ISBN 0-262-03149-3. MR 1104662 （英语）.  网址－维基内链冲突 (帮助)
• Howe, Roger. On the tendency toward convexity of the vector sum of sets [論集合的向量和趨向凸] (PDF) (报告) 538. New Haven, Conn.: Cowles Foundation for Research in Economics, Yale University. 3 November 1979 [1 January 2011]. （原始内容存档 (PDF)于2011-08-07） （英语）. 
• Mas-Colell, A. Non-convexity [非凸性]. Eatwell, John; Milgate, Murray; Newman, Peter (编). The new Palgrave: A dictionary of economics [新帕爾格雷夫經濟學詞典] first. Palgrave Macmillan. 1987: 653–661 [2021-08-31]. ISBN 9780333786765. doi:10.1057/9780230226203.3173. (Mas-Colell個人主頁的PDF檔). （原始内容存档于2017-11-21） （英语）. 
• Rockafellar, R. Tyrrell. Convex analysis [凸分析]. Princeton Landmarks in Mathematics. Princeton, N.J.: Princeton University Press. 1997: xviii+451. ISBN 0-691-01586-4. MR 1451876 （英语）.  1970年(MR274683) Princeton Mathematical Series 28的重印版。
• Schneider, Rolf. Convex bodies: The Brunn–Minkowski theory [凸體：布倫-閔可夫斯基理論]. Encyclopedia of Mathematics and its Applications 44. Cambridge, UK: Cambridge University Press. 1993: xiv+490. ISBN 0-521-35220-7. MR 1216521 （英语）. 
• Starr, Ross M. Quasi-equilibria in markets with non-convex preferences (Appendix 2: The Shapley–Folkman theorem, pp. 35–37) [有非凸偏好的市場的準均衡（附錄2:沙普利-福克曼定理，pp. 35–37）]. Econometrica. 1969, 37 (1): 25–38. JSTOR 1909201. doi:10.2307/1909201 （英语）. 
• Starr, Ross M. 8 Convex sets, separation theorems, and non-convex sets in R^N (new chapters 22 and 25–26 in (2011) second ed.) [第8章：R^N中的凸集、分離定理、非凸集（及2011年第二版新增的第22、25、26諸章）]. General equilibrium theory: An introduction [一般均衡理論：導論] First. Cambridge, UK: Cambridge University Press. 1997: xxiii+250. ISBN 0-521-56473-5. MR 1462618 （英语）. 
• Starr, Ross M. Shapley–Folkman theorem [沙普利-福克曼定理]. Durlauf, Steven N.; Blume, Lawrence E (编). The new Palgrave dictionary of economics [新帕爾格雷夫經濟學詞典] Second. Palgrave Macmillan. 2008: 317–318 (1st ed.) [2021-08-31]. ISBN 978-0-333-78676-5. doi:10.1057/9780230226203.1518. （原始内容存档于2017-03-16） （英语）. 

• Anderson, Robert M. Nonconvex preferences and approximate equilibria [非凸偏好與近似均衡] (PDF). Economics 201B: Economic Theory (Handouts) [經濟學201B: 經濟理論（課堂講義）]. Robert M. Anderson's homepage (Berkeley, Calif.). 14 March 2005: 1–5 [1 January 2011]. （原始内容存档 (PDF)于2012-03-10）. 
• Starr, Ross M. 8 Convex sets, separation theorems, and non-convex sets in R^N (Section 8.2.3 Measuring non-convexity, the Shapley–Folkman theorem) [第8章：R^N中的凸集、分離定理、非凸集（第8.2.3小節：量度非凸性、沙普利-福克曼定理）] (PDF). General equilibrium theory: An introduction [一般均衡理論：導論]. September 2009: 3–6 [2021-08-31]. ISBN 9781139174749. MR 1462618. doi:10.1017/CBO9781139174749. （第二版的書稿，來自斯塔在加州大學聖地亞哥分校經濟學系的課程）. （原始内容存档 (PDF)于2010-07-01） （英语）. 
• Starr, Ross M. Shapley–Folkman theorem [沙普利-福克曼定理]. Durlauf, Steven N.; Blume, Lawrence E (编). The new Palgrave dictionary of economics [新帕爾格雷夫經濟學詞典] Second. Palgrave Macmillan. 2008: 317–318 (1st ed.) [2021-08-31]. ISBN 978-0-333-78676-5. doi:10.1057/9780230226203.1518. （原始内容存档于2017-03-16） （英语）.