计算复杂性理论 (Computational complexity theory)是理论计算机科学 和数学的一个分支,它致力于将可计算问题根据它们本身的复杂性 分类,以及将这些类别联系起来。一个可计算问题被认为是一个原则上可以用计算机解决的问题,亦即这个问题可以用一系列机械的数学步骤解决,例如算法 。
如果一个问题的求解需要相当多的资源(无论用什么算法),则被认为是难解的。计算复杂性理论通过引入数学计算模型来研究这些问题以及定量计算解决问题所需的资源(时间和空间),从而将资源的确定方法正式化了。其他复杂性测度同样被运用,比如通信量(应用于通信复杂性),电路中门的数量(应用于电路复杂性)以及中央处理器的数量(应用于并行计算)。计算复杂性理论的一个作用就是确定一个能或不能被计算机求解的问题的所具有的实际限制。
在理论计算机科学领域,与此相关的概念有算法分析和可计算性理论。两者之间一个关键的区别是前者致力于分析用一个确定的算法来求解一个问题所需的资源量,而后者则是在更广泛意义上研究用所有可能的算法来解决相同问题。更精确地说,它尝试将问题分成能或不能在现有的适当受限的资源条件下解决这两类。相应地,在现有资源条件下的限制正是区分计算复杂性理论和可计算性理论的一个重要指标:后者关心的是何种问题原则上可以用算法解决。
计算复杂性理论所研究的资源中最常见的是时间(要通过多少步演算 才能解决问题)和空间(在解決問題時需要多少記憶體 )。其他資源亦可考慮,例如在并行计算 中,需要多少并行處理器才能解決問題。
時間複雜度是指在電腦科學 與工程領域完成一個演算法 所需要的時間,是衡量一個演算法優劣的重要參數。時間複雜度越小,說明該演算法效率越高,則該演算法越有價值。
空間複雜度是指電腦科學領域完成一個演算法所需要占用的存儲空間 ,一般是輸入參數的函數。它是演算法優劣的重要度量指標,一般來說,空間複雜度越小,演算法越好。我們假設有一個圖靈機 來解決某一類語言的某一問題,設有
X
{\displaystyle X}
X
{\displaystyle X}
空間 。
複雜度理論和可计算性理论 不同,可计算性理論的重心在於問題能否解決,不管需要多少資源。而复杂性理论作为计算理论的分支,某种程度上被认为和算法理论是一种“矛”与“盾”的关系,即算法理论专注于设计有效的算法,而复杂性理论专注于理解为什么对于某类问题,不存在有效的算法。
在20世纪50年代,Trahtenbrot和Rabin的论文被认为是该领域最早的文献。而一般说来,被公认为奠定了计算复杂性领域基础的是Hartmanis和Stearns的1960年代的论文On the computational complexity of algorithms。在这篇论文中,作者引入了时间复杂性类
TIME
(
f
(
n
)
)
{\displaystyle {\text{TIME}}(f(n))}
对角线法 证明了时间层级定理 (Time Hierarchy Theorem)。
在此之后,许多研究者对复杂性理论作出了贡献。期间重要的发现包括:对随机算法 的去随机化 (derandomization)的研究,对近似算法 的不可近似性 (hardness of approximation)的研究,以及交互式证明系统 理论和零知识证明 (Zero-knowledge proof)等。特别的复杂性理论对近代密码学 的影响非常显著,而最近,复杂性理论的研究者又进入了博弈论 领域,并创立了“算法博弈论 ”(algorithmic game theory)这一分支。
计算复杂性理论的研究对象是算法 在执行时所需的计算资源 ,而为了讨论这一点,我们必须假设算法是在某个计算模型 上运行的。常讨论的计算模型包括图灵机 (Turing machine)和电路 (circuit),它们分别是一致性 (uniform)和非一致性 (non-uniform)计算模型的代表。而计算资源与计算模型是相关的,如对图灵机我们一般讨论的是时间、空间和随机源,而对电路我们一般讨论电路的大小。
由邱奇-图灵论题 (Church-Turing thesis),所有的一致的计算模型与图灵机在多项式时间 意义下是等价的。而由于我们一般将多项式时间作为有效算法的标志,该论题使得我们可以仅仅关注图灵机而忽略其它的计算模型。
我们考虑对一个算法问题,什么样的回答是我们所需要的。比如搜索问题:给定数组
A
{\displaystyle A}
s
{\displaystyle s}
s
{\displaystyle s}
A
{\displaystyle A}
s
{\displaystyle s}
A
{\displaystyle A}
s
{\displaystyle s}
二分图
G
=
(
V
,
E
)
{\displaystyle G=(V,E)}
E
{\displaystyle E}
E
{\displaystyle E}
E
{\displaystyle E}
自然的,我们会发现对于一般的算法问题
A
{\displaystyle A}
A
{\displaystyle A}
A
{\displaystyle A}
A
{\displaystyle A}
A
{\displaystyle A}
A
{\displaystyle A}
A
{\displaystyle A}
可计算性理论 和计算复杂性理论中有着不同的回答,这也是理解计算复杂性理论与它的前身可计算性理论不同的一个基本的观察。
在可计算性理论 中,可以说明,判定型问题和搜索型问题在可计算性的意义下是等价的。而在计算复杂性中,Khuller和Vazirani在1990年代证明了在P≠NP的假设下,平面图4-着色问题的判定型问题是在P中的,而寻找其字典序第一的着色是NP难的。[ 1]
所以在可计算性理论中,只关注判定型问题是合理的。在计算复杂性理论中,虽然一些基本的复杂性类(如P,NP和PSPACE),以及一些基本的问题(P和NP关系问题等)是用判定型问题来定义的,但函数型问题复杂性类也被定义(如FP,FNP等),而且一些特别的函数型问题复杂性类,如TFNP,也正在逐渐受到关注。
上面提到计算复杂性理论的研究对象是执行一项计算任务所用的资源,特别的,时间和空间是最重要的两项资源。
我们用时间作例子来讨论算法分析的一些基础知识。如果将输入的长度(设为
n
{\displaystyle n}
n
{\displaystyle n}
T
(
n
)
{\displaystyle T(n)}
T
(
n
)
{\displaystyle T(n)}
可计算性理论 ),我们使用大O表达式 来表示
T
(
n
)
{\displaystyle T(n)}
以搜索这个计算任务为例。在搜索问题中,给定了一个具体的数
s
{\displaystyle s}
n
{\displaystyle n}
A
{\displaystyle A}
n
{\displaystyle n}
s
{\displaystyle s}
A
{\displaystyle A}
s
{\displaystyle s}
s
{\displaystyle s}
A
{\displaystyle A}
n
+
1
{\displaystyle n+1}
A
{\displaystyle A}
s
{\displaystyle s}
如果我们假设
s
{\displaystyle s}
A
{\displaystyle A}
機率 都相同,那么算法在找到
s
{\displaystyle s}
1
n
(
1
+
2
+
⋯
+
n
)
=
n
(
n
+
1
)
2
n
=
n
+
1
2
{\displaystyle {\frac {1}{n}}(1+2+\cdots +n)={\frac {n(n+1)}{2n}}={\frac {n+1}{2}}}
s
{\displaystyle s}
A
{\displaystyle A}
(
n
+
1
)
{\displaystyle (n+1)}
O
(
n
)
{\displaystyle O(n)}
而如果我们进一步假设
A
{\displaystyle A}
二分查找算法 ,使得算法的运行时间是
O
(
log
n
)
{\displaystyle O(\log n)}
将计算问题按照在不同计算模型下所需资源的不同予以分类,从而得到一个对算法问题“难度”的类别,就是复杂性理论中复杂性类概念的来源。例如一个问题如果在确定性图灵机上所需时间不会超过一个确定的多项式(以输入的长度为多项式的不定元),那么我们称这类问题的集合为P(polynomial time Turing machine)。而将前述定义中的“确定性图灵机”改为“不确定性图灵机”,那么所得到的问题集合为NP(non-deteministic polynomial time Turing machine)。类似的,设
n
{\displaystyle n}
O
(
log
n
)
{\displaystyle O(\log n)}
L
{\displaystyle L}
O
(
log
n
)
{\displaystyle O(\log n)}
O
(
1
)
{\displaystyle O(1)}
1 )等等复杂性类。
定义复杂性类问题的目的是为了将所有的算法问题进行分类,以确定当前算法的难度,和可能的前进方向。这是复杂性理论的一个主线之一:对算法问题进行抽象和分类。例如透过大O表达式,我们可以对忽略因计算模型不同而引入的常数因子。而第二个重要的理论假设,就是将多项式时间作为有效算法的标志(与之对应的是指数时间)。这样,复杂性类使得我们可以忽略多项式阶的不同而專注于多项式时间和指数时间的差别。(对多项式时间作为有效算法的标志这一点是有一定争议的,比如,如果算法的运行时间
n
10
{\displaystyle n^{10}}
理论与实践 。)在本文的其余章节,“有效算法”等价于“多项式算法”
归约 (reduction)是将不同算法问题建立联系的主要的技术手段,并且在某种程度上,定义了算法问题的相对难度。简单来说,假设我们有算法任务
A
{\displaystyle A}
B
{\displaystyle B}
A
{\displaystyle A}
B
{\displaystyle B}
A
≤
B
{\displaystyle A\leq B}
B
{\displaystyle B}
M
{\displaystyle M}
N
{\displaystyle N}
M
{\displaystyle M}
A
{\displaystyle A}
我们以点集覆盖问题 (vertex cover)和独立集问题 (independent set)为例来进行说明。这两个问题都是图论 中的问题。假设给定了无向图
G
=
(
V
,
E
)
{\displaystyle G=(V,E)}
k
{\displaystyle k}
V
{\displaystyle V}
S
{\displaystyle S}
∀
e
∈
E
{\displaystyle \forall e\in E}
s
∈
S
{\displaystyle s\in S}
s
∈
e
{\displaystyle s\in e}
|
S
|
≤
k
{\displaystyle |S|\leq k}
V
{\displaystyle V}
S
{\displaystyle S}
∀
s
1
,
s
2
∈
S
,
(
s
1
,
s
2
)
∉
E
{\displaystyle \forall s_{1},s_{2}\in S,(s_{1},s_{2})\notin E}
|
S
|
≤
k
{\displaystyle |S|\leq k}
一个简单的观察即是:对
G
=
(
V
,
E
)
{\displaystyle G=(V,E)}
S
⊂
V
{\displaystyle S\subset V}
S
{\displaystyle S}
G
{\displaystyle G}
补图 中是独立点集(而且保持集合大小)。利用这个观察,假设我们有了解决覆盖点集问题的算法
M
{\displaystyle M}
算法
N
{\displaystyle N}
输入:给定无向图
G
=
(
V
,
E
)
{\displaystyle G=(V,E)}
k
{\displaystyle k}
输出:一个大小小于等于
k
{\displaystyle k}
已知:算法
M
{\displaystyle M}
G
{\displaystyle G}
k
{\displaystyle k}
k
{\displaystyle k}
算法步骤:
对
G
{\displaystyle G}
G
{\displaystyle G}
G
′
{\displaystyle G'}
调用
M
{\displaystyle M}
(
G
′
,
k
)
{\displaystyle (G',k)}
如果
M
{\displaystyle M}
M
{\displaystyle M}
S
⊂
V
{\displaystyle S\subset V}
S
{\displaystyle S}
可以看出若产生补图这一步是有效的,那么如果
M
{\displaystyle M}
N
{\displaystyle N}
B
{\displaystyle B}
M
{\displaystyle M}
B
{\displaystyle B}
A
{\displaystyle A}
N
{\displaystyle N}
N
{\displaystyle N}
A
{\displaystyle A}
N
′
{\displaystyle N'}
N
{\displaystyle N}
M
{\displaystyle M}
所以从归约的观点来看,下面的说法可以看作与“
A
{\displaystyle A}
B
{\displaystyle B}
A
≤
B
{\displaystyle A\leq B}
A
{\displaystyle A}
B
{\displaystyle B}
A
{\displaystyle A}
B
{\displaystyle B}
A
{\displaystyle A}
B
{\displaystyle B}
A
{\displaystyle A}
B
{\displaystyle B}
存在通过查询
B
{\displaystyle B}
A
{\displaystyle A}
B
{\displaystyle B}
A
{\displaystyle A}
计算复杂性理论最成功的成果之一是NP完备 理论。通过该理论,我们可以理解为什么在程序设计与生产实践中遇到的很多问题至今没有找到多项式算法。而该理论更为计算复杂性中的核心问题:P与NP的关系问题指明了方向。
在上面我们已经知道,NP是指“在非确定性图灵机上有多项式时间算法的问题”的集合,而P是指“在确定性图灵机上有多项式时间算法的问题”的集合。这里我们都考虑的是判定型问题,即考虑一个语言
L
{\displaystyle L}
x
{\displaystyle x}
L
{\displaystyle L}
L
{\displaystyle L}
x
{\displaystyle x}
w
{\displaystyle w}
(
x
,
w
)
{\displaystyle (x,w)}
L
{\displaystyle L}
x
{\displaystyle x}
x
{\displaystyle x}
L
{\displaystyle L}
举个例子,就是考虑完美匹配问题、点集覆盖问题和图不同构问题。这三个问题都有图论背影,问题的描述如下:
完美匹配问题:给定图
G
=
(
V
,
E
)
{\displaystyle G=(V,E)}
F
⊂
E
{\displaystyle F\subset E}
v
∈
V
{\displaystyle v\in V}
e
∈
F
,
v
∈
e
{\displaystyle e\in F,v\in e}
点集覆盖问题:给定图
G
=
(
V
,
E
)
{\displaystyle G=(V,E)}
k
{\displaystyle k}
U
⊂
V
{\displaystyle U\subset V}
e
∈
E
{\displaystyle e\in E}
v
∈
U
,
v
∈
e
{\displaystyle v\in U,v\in e}
|
U
|
≤
k
{\displaystyle |U|\leq k}
图不同构问题:给定图
G
=
(
V
,
E
)
,
H
=
(
U
,
F
)
,
|
G
|
=
|
H
|
{\displaystyle G=(V,E),H=(U,F),|G|=|H|}
G
{\displaystyle G}
H
{\displaystyle H}
∃
T
:
V
→
U
{\displaystyle \exists T:V\rightarrow U}
s
,
t
∈
V
{\displaystyle s,t\in V}
E
(
s
,
t
)
=
F
(
T
(
s
)
,
T
(
t
)
)
{\displaystyle E(s,t)=F(T(s),T(t))}
E
{\displaystyle E}
V
×
V
→
{
0
,
1
}
{\displaystyle V\times V\rightarrow \{0,1\}}
G
{\displaystyle G}
H
{\displaystyle H}
不存在 这样的映射。 关于这三个问题,它们在复杂性理论中,目前的地位如下:
完美匹配问题:在P中。可以利用艾德蒙德算法
O
(
V
E
)
{\displaystyle O({\sqrt {V}}E)}
点集覆盖问题:在NP中,而不知道是否在P中。实际上,它是NP完备问题,给出它的多项式算法将意味着证明NP=P。它在NP中,原因是给定一个点的子集
U
⊂
V
{\displaystyle U\subset V}
|
U
|
≤
k
{\displaystyle |U|\leq k}
U
{\displaystyle U}
e
{\displaystyle e}
U
{\displaystyle U}
v
{\displaystyle v}
v
∈
e
{\displaystyle v\in e}
O
(
V
E
)
{\displaystyle O(VE)}
图不同构问题:在AM中,而不知道是否在NP中。它之所以困难,一个直观的想法是:给定两个图
G
{\displaystyle G}
H
{\displaystyle H}
≤
k
≤
|
V
|
{\displaystyle \leq k\leq |V|}
T
:
V
→
U
{\displaystyle T:V\rightarrow U}
这样我们有了:在P中、在NP而不知道是不是在P中、在AM中而不知道是不是在NP中的三个问题。
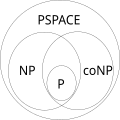
在P ≠ NP 前提下复杂性类的关系图解。在该前提下,不在P也不是NP完备的问题的存在性由Ladner解决。[ 2] 由于在多项式时间可以判断
x
{\displaystyle x}
L
{\displaystyle L}
x
{\displaystyle x}
L
{\displaystyle L}
L
∈
{\displaystyle L\in }
L
∉
{\displaystyle L\notin }
NP完备 理论赋予了它在实践上的重要性,有证明复杂性 理论赋予了它纯数学理论上的重要性,有PCP理论 和NP完备 理论赋予了它算法理论上的重要性。这些理论或者在根本上依赖于NP和P关系问题的某些假设,或者本身就是试图去理解NP和P关系问题而发展出来的,这使得它成为了理论计算机科学 乃至数学的中心问题之一。在2000年,克雷数学研究所 提出了新世纪的数学中七个中心问题,NP与P关系问题就是其中的一个。
关于NP与P关系问题最早发展出的理论是NP完备理论。我们在下面一节简单了解NP完备理论。
由上面归约的知识我们知道,算法问题之间可以根据归约来定义相对的难度。即对问题
A
{\displaystyle A}
B
{\displaystyle B}
A
{\displaystyle A}
B
{\displaystyle B}
A
≤
B
{\displaystyle A\leq B}
B
{\displaystyle B}
A
{\displaystyle A}
M
{\displaystyle M}
M
{\displaystyle M}
A
∈
{\displaystyle A\in }
∀
B
∈
{\displaystyle \forall B\in }
B
≤
A
{\displaystyle B\leq A}
这个问题乍看起来很不容易把握。因为这需要对所有的NP中的语言L,去找到一个L到A的归约算法。然而1970年代的由史蒂芬·库克 和列昂尼德·列文 分别发现的库克-列文定理 ,证明了布尔表达式 (Boolean formula)的可满足性问题 (SAT问题)是NP完备的。概括的说,他们证明了,有一个通用的过程对NP中任意语言在非确定性图灵机上运行历史用布尔表达式来编码,使得该布尔表达式是可满足的,当且仅当该运行历史是对给定输入,接受该输入的。这样,我们就有了第一个被证明是NP完备的问题。
在库克给出SAT问题是NP完备之后不久,理查德·卡普 证明了21个图论 、组合数学 中常见的问题都是NP完备的。这赋予了NP完备问题在实践中的重要性。现在,已经有成千个在实践中遇到的算法问题被证明是NP完备的(参见NP完备问题列表 ),特别的有许多问题,如旅行商问题 等的最优算法会带来很大的经济效益(旅行商问题的最优解可以给出最优的电路布线方案,而SAT的最优算法会促进程序验证等问题的进步)。由NP完备的定义,我们知道对这其中任何一个问题的多项式算法都将给出所有NP问题,也包括所有NP完备问题的多项式算法。然而尽管实际问题中遇到很多NP完备的问题,而且有很多问题在不同领域有着相当的重要性而被大量研究,至今,仍没有对NP完备问题的多项式算法,这是一些理论计算机科学家认为NP≠P的理由之一。
对NP和P关系问题,NP完备理论给出了如下的暗示:如果要证明NP=P,一个可能的方向是对NP完备问题给出多项式算法;如果要证明NP≠P,那么必然的一个结果是NP完备问题没有多项式算法。
电路复杂性 理论在1990年代以前,被众多研究者认为是解决NP与P关系问题的可能的途径之一。电路复杂性研究的对象是非一致性的计算模型电路 ,并考虑计算一个布尔函数 所需的最小的电路的深度(depth)和大小(size)等资源。其中,大小为多项式大小的电路族可以计算的布尔函数被记为P/poly 。可以证明,P包含在P/poly之中,而卡普-利普顿定理 (Karp-Lipton theorem)表明若P/poly在NP之中,则多项式层级 (polynomial hierarchy)将会坍缩至第二层,这是一个不大可能的结果。这两个结果结合起来表明,P/poly可以当作是分离NP与P的一个中间的工具,具体的途径就是证明任一个NP完全问题的电路大小的下界。在直观上说,电路复杂性也绕过了NP与P问题的第一个困难:相对化证明困难 (relativizing proofs)。
在1980年代,电路复杂性途径取得了一系列的成功,其中包括奇偶性函数 (Parity function)在
A
C
0
{\displaystyle AC^{0}}
团问题 (clique problem)在单调性电路 (monotone circuit)中的下界为指数。然而在1994年Razborov Rudich 自然性证明 (Natural proof)中指出,上面所用证明电路下界的方法,在单向函数 存在的前提下是不可能分离NP和P的。该结果使很多专家对证明电路下界来分离NP和P的前景表示不乐观。
计算复杂性的初衷是理解不同算法问题的难度,特别的是一些重要算法问题的困难性。为了确切的描述一个问题的困难性,计算复杂性的第一步抽象是认为多项式时间是有效的,非多项式时间是困难的。这基于指数函数 增长速度的“违反直觉”的特性:如果一个算法的时间复杂性为
2
n
{\displaystyle 2^{n}}
10
12
{\displaystyle 10^{12}}
CPU 速度,参见Instructions per second ,其中报告截止2009年,主流个人电脑的运算速度可以看作是
4
×
10
10
{\displaystyle 4\times 10^{10}}
4
×
10
10
{\displaystyle 4\times 10^{10}}
宇宙年龄 。这为多项式时间被看作是有效时间提供了直观上的证据。
然而多项式的指数很大的时候,算法在实践中也不能看作是有效的。如
n
10
{\displaystyle n^{10}}
2
100
{\displaystyle 2^{100}}
近似算法 ),或有很好的启发式算法 (heuristics)。启发式算法的特点是在理论上没有精确的行为的分析,或者可以表明存在很坏的输入,在这些输入上运行很慢。然而在大多数时候,它都能快速解决问题。计算复杂性中对应的理论分析是平均复杂性理论 (average-case complexity theory)和光滑分析 (smooth analysis)。实际中的例子包括Presburger arithmetic 布尔可满足性问题 (参见SAT solver )和背包问题 。
書籍 Arora, Sanjeev ; Barak, Boaz, Computational Complexity: A Modern Approach , Cambridge , 2009 [2018-06-22 ] , ISBN 978-0-521-42426-4Zbl 1193.68112 存档 于2021-03-20) Downey, Rod; Fellows, Michael , Parameterized complexity , Berlin, New York: Springer-Verlag , 1999 [失效連結 Du, Ding-Zhu; Ko, Ker-I, Theory of Computational Complexity, John Wiley & Sons , 2000, ISBN 978-0-471-34506-0 Template:Garey-Johnson Goldreich, Oded , Computational Complexity: A Conceptual Perspective , Cambridge University Press, 2008 [2018-06-22 ] , (原始内容 存档于2021-11-08) van Leeuwen, Jan (编), Handbook of theoretical computer science (vol. A): algorithms and complexity, MIT Press , 1990, ISBN 978-0-444-88071-0 Papadimitriou, Christos , Computational Complexity 1st, Addison Wesley, 1994, ISBN 0-201-53082-1 Sipser, Michael , Introduction to the Theory of Computation 2nd, USA: Thomson Course Technology , 2006, ISBN 0-534-95097-3 期刊文章 Khalil, Hatem; Ulery, Dana , A Review of Current Studies on Complexity of Algorithms for Partial Differential Equations , Proceedings of the annual conference on - ACM 76 (ACM '76 Proceedings of the 1976 Annual Conference), 1976: 197, doi:10.1145/800191.805573 Cook, Stephen , An overview of computational complexity (PDF) , Commun. ACM (ACM), 1983, 26 (6): 400–408 [2018-06-22 ] , ISSN 0001-0782 doi:10.1145/358141.358144 原始内容 (PDF) 存档于2018-07-22) Fortnow, Lance; Homer, Steven, A Short History of Computational Complexity (PDF) , Bulletin of the EATCS, 2003, 80 : 95–133 [2018-06-22 ] , (原始内容存档 (PDF) 于2021-03-20) Mertens, Stephan, Computational Complexity for Physicists, Computing in Science and Eng. (Piscataway, NJ, USA: IEEE Educational Activities Department), 2002, 4 (3): 31–47, ISSN 1521-9615 arXiv:cond-mat/0012185 doi:10.1109/5992.998639
易解复杂度类
怀疑难解复杂度类 难解复杂度类 复杂度类的谱系 相关复杂度族