еӨ§еҚҒдәҢйқўеҚҠеҚҒдәҢйқўй«”
еӨ§еҚҒдәҢйқўеҚҠеҚҒдәҢйқўй«” жҳҜдёҖ種擬жӯЈеҚҠеӨҡйқўй«” [ 1] дә”и§’жҳҹ йқўе’Ң6еҖӢз©ҝйҒҺж•ҙй«”е№ҫдҪ•дёӯеҝғ зҡ„еҚҒи§’жҳҹ йқўзө„жҲҗпјҢ[ 2] [ 3] еӨ§жҲӘеҚҠдәҢеҚҒйқўдҪ“ 經йҒҺеҲ»йқў [ 4] еӨ§жҲӘеҚҠдәҢеҚҒйқўдҪ“ зӣёеҗҢпјҢзҡҶзӮәжҲӘеҚҠеҚҒдәҢйқўй«” [ 5] Albert Badoureau [ 6]
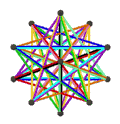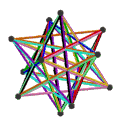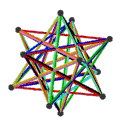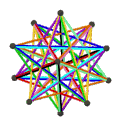
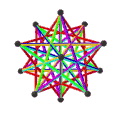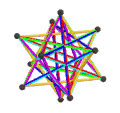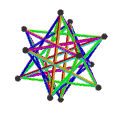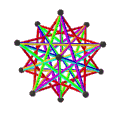
еӨ§еҚҒдәҢйқўеҚҠеҚҒдәҢйқўй«”з”ұ18еҖӢйқў гҖҒ60жўқйӮҠ е’Ң30еҖӢй Ӯй»һ зө„жҲҗгҖӮеңЁе…¶18еҖӢйқўдёӯжңү12еҖӢдә”и§’жҳҹ йқўе’Ң6еҖӢеҚҒи§’жҳҹ йқўпјӣе…¶дёӯ12еҖӢдә”и§’жҳҹ йқўеҸҲеҸҜд»ҘеҶҚеҲҶжҲҗ2зө„пјҢеҲҶеҲҘд»ҘзӣёеҸҚзҡ„ж–№ејҸзӣёжҺҘпјҢеңЁж–ҪиҗҠеӨ«еҲ©з¬Ұиҷҹ дёӯеҲҶеҲҘиЁҳзӮә{5/2}еҸҠ{5/3}[ 7] жӯЈеҚҒдәҢйқўй«” пјҢдё”е…¶ж•ёйҮҸжӯЈеҘҪжҳҜжӯЈеҚҒдәҢйқўй«”зҡ„дёҖеҚҠ[ 8] [ 8] еҚҠеӨҡйқўй«” гҖӮ[ 9] [ 10]
еӨ§еҚҒдәҢйқўеҚҠеҚҒдәҢйқўй«”еҸҜд»ҘиҰ–зӮәеӨ§жҲӘеҚҠдәҢеҚҒйқўдҪ“ 經йҒҺеҲ»йқў [ 4] еӨ§жҲӘеҚҠдәҢеҚҒйқўй«” й Ӯй»һеә§жЁҷд№ҹжңғзӣёеҗҢ[ 11] [ 12] [ 11]
(
Вұ
5
вҲ’
1
2
,
0
,
0
)
{\displaystyle \left(\pm {\frac {{\sqrt {5}}-1}{2}},\,0,\,0\right)}
(
0
,
Вұ
5
вҲ’
1
2
,
0
)
{\displaystyle \left(0,\,\pm {\frac {{\sqrt {5}}-1}{2}},\,0\right)}
(
0
,
0
,
Вұ
5
вҲ’
1
2
)
{\displaystyle \left(0,\,0,\,\pm {\frac {{\sqrt {5}}-1}{2}}\right)}
(
Вұ
5
вҲ’
1
4
,
Вұ
1
2
,
Вұ
3
вҲ’
5
4
)
{\displaystyle \left(\pm {\frac {{\sqrt {5}}-1}{4}},\,\pm {\frac {1}{2}},\,\pm {\frac {3-{\sqrt {5}}}{4}}\right)}
(
Вұ
1
2
,
Вұ
3
вҲ’
5
4
,
Вұ
5
вҲ’
1
4
)
{\displaystyle \left(\pm {\frac {1}{2}},\,\pm {\frac {3-{\sqrt {5}}}{4}},\,\pm {\frac {{\sqrt {5}}-1}{4}}\right)}
(
Вұ
3
вҲ’
5
4
,
Вұ
5
вҲ’
1
4
,
Вұ
1
2
)
{\displaystyle \left(\pm {\frac {3-{\sqrt {5}}}{4}},\,\pm {\frac {{\sqrt {5}}-1}{4}},\,\pm {\frac {1}{2}}\right)}
[ 11]
еӨ§еҚҒдәҢйқўеҚҠеҚҒдәҢйқўй«”еҸӘжңүдёҖзЁ®дәҢйқўи§’ пјҢзӮәдә”и§’жҳҹе’ҢеҚҒи§’жҳҹзҡ„дәҢйқўи§’[ 4] еҸҚйӨҳејҰ еҖјпјҡ[ 13]
cos
вҲ’
1
вҒЎ
5
5
вүҲ
1.10714872
вүҲ
63.4349488
вҲҳ
{\displaystyle \cos ^{-1}{\frac {\sqrt {5}}{5}}\approx 1.10714872\approx 63.4349488^{\circ }}
еӨ§еҚҒдәҢйқўеҚҠеҚҒдәҢйқўй«”иҲҮеӨ§дәҢеҚҒйқўеҚҠеҚҒдәҢйқўй«” еҸҠеӨ§жҲӘеҚҠдәҢеҚҒйқўдҪ“ е…ұз”ЁзӣёеҗҢзҡ„й Ӯй»һжҺ’еҲ—ж–№ејҸ[ 14] [ 15] [ 15] зҡ®зү№йҮҢеӨ§дәҢеҚҒйқўй«” пјҲеӨ§дәҢеҚҒйқўй«” зҡ„зҡ®зү№йҮҢе°ҚеҒ¶ пјүгҖҒеӨ§дәҢеҚҒйқўеҚҠеҚҒдәҢйқўй«”еҸҜд»ҘиҰ–зӮәжҳҜжҲӘеҚҠзҡ„зҡ®зү№йҮҢеӨ§жҳҹеҪўеҚҒдәҢйқўй«”пјҲеӨ§жҳҹеҪўеҚҒдәҢйқўй«” зҡ„зҡ®зү№йҮҢе°ҚеҒ¶ пјүгҖӮ[ 2]
зҡ®зү№йҮҢеӨ§дәҢеҚҒйқўй«”жҳҜеӨ§дәҢеҚҒйқўй«” зҡ„зҡ®зү№йҮҢе°ҚеҒ¶ пјҢеҸҜд»ҘйҖҸйҒҺе°ҮеҺҹжңүеӨ§дәҢеҚҒйқўй«”дёҠеҸ–зҡ®зү№йҮҢеӨҡйӮҠеҪў ж§ӢжҲҗпјҢжҸӣеҸҘи©ұиӘӘпјҢзҡ®зү№йҮҢеӨ§дәҢеҚҒйқўй«”зӮәз”ұеӨ§дәҢеҚҒйқўй«”зҡ„зҡ®зү№йҮҢеӨҡйӮҠеҪўж§ӢжҲҗзҡ„з«Ӣй«”[ 16] [ 17]
еӨ§дәҢеҚҒйқўй«”е°ҚжҮүзҡ„жӯЈеүҮең°еҚҖең–иҲҮжӯЈдәҢеҚҒйқўй«”еҗҢж§Ӣ[ 18] зҡ®зү№йҮҢдәҢеҚҒйқўй«” еҗҢж§ӢпјҢдё”е°ҚжҮүзҡ„йӘЁжһ¶ең–зҡҶзӮәдәҢеҚҒйқўй«”ең–[ 19]
зҡ®зү№йҮҢеӨ§жҳҹеҪўеҚҒдәҢйқўй«” гҖҒеӨ§жҳҹеҪўеҚҒдәҢйқўй«” гҖҒеӨ§дәҢеҚҒйқўй«” гҖҒзҡ®зү№йҮҢеӨ§дәҢеҚҒйқўй«” зҡ„й—ңдҝӮеҰӮдёӢпјҡ[ 20]
{
6
,
5
2
}
{\displaystyle \left\{6,\,{\frac {5}{2}}\right\}}
зҡ®зү№йҮҢеӨ§еҚҒдәҢйқўй«”
вҶ”
ПҖ
{\displaystyle {\ce {<->[\pi]}}}
{
5
,
5
2
}
{\displaystyle \left\{5,\,{\frac {5}{2}}\right\}}
еӨ§еҚҒдәҢйқўй«”
вҶ”
Оҙ
{\displaystyle {\ce {<->[\delta]}}}
{
5
2
,
5
}
{\displaystyle \left\{{\frac {5}{2}},\,5\right\}}
е°ҸжҳҹеҪўеҚҒдәҢйқўй«”
вҶ”
ПҖ
{\displaystyle {\ce {<->[\pi]}}}
{
6
,
5
}
{\displaystyle \left\{6,\,5\right\}}
зҡ®зү№йҮҢе°ҸжҳҹеҪўеҚҒдәҢйқўй«”
вҶ•
ПҶ
2
{\displaystyle \varphi _{2}}
{
10
3
,
3
}
{\displaystyle \left\{{\frac {10}{3}},\,3\right\}}
зҡ®зү№йҮҢеӨ§жҳҹеҪўеҚҒдәҢйқўй«”
вҶ”
ПҖ
{\displaystyle {\ce {<->[\pi]}}}
{
5
2
,
3
}
{\displaystyle \left\{{\frac {5}{2}},\,3\right\}}
еӨ§жҳҹеҪўеҚҒдәҢйқўй«”
вҶ”
Оҙ
{\displaystyle {\ce {<->[\delta]}}}
{
3
,
5
2
}
{\displaystyle \left\{3,\,{\frac {5}{2}}\right\}}
еӨ§дәҢеҚҒйқўй«”
вҶ”
ПҖ
{\displaystyle {\ce {<->[\pi]}}}
{
10
3
,
5
2
}
{\displaystyle \left\{{\frac {10}{3}},\,{\frac {5}{2}}\right\}}
зҡ®зү№йҮҢеӨ§дәҢеҚҒйқўй«”
е…¶дёӯпјҢгҖҢ
вҶ”
ПҖ
{\displaystyle {\ce {<->[\pi]}}}
зҡ®зү№йҮҢе°ҚеҒ¶ пјӣгҖҢ
вҶ”
Оҙ
{\displaystyle {\ce {<->[\delta]}}}
е°ҚеҒ¶еӨҡйқўй«” пјӣгҖҢ
вҶ”
ПҶ
{\displaystyle {\ce {<->[\varphi]}}}
еӨ§еҚҒдәҢйқўеҚҠеҚҒдәҢйқўй«”еҸҜд»ҘиҰ–зӮәжҳҜйҖЈжҺҘзҡ®зү№йҮҢеӨ§дәҢеҚҒйқўй«”жҜҸеҖӢйӮҠзҡ„дёӯй»һ ж§ӢжҲҗзҡ„з«Ӣй«”гҖӮ[ 2]
^ David I. McCooey. Versi-Regular Polyhedra . dmccooey.com. [2021-09-05 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2021-07-30пјү. ^ 2.0 2.1 2.2 Weiss, Asia IviДҮ and Schulte, Egon. Hereditary polyhedra with planar regular faces. The Art of Discrete and Applied Mathematics. 2020, 3 (2): 2вҖ“07. ^ Vladimir Bulatov. great dodecahemidodecahedron . [2021-09-06 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2021-02-28пјү. ^ 4.0 4.1 4.2 Klitzing, Richard. great dodecahemidodecahedron : gidhid . bendwavy.org. [2021-09-05 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2021-01-23пјү. ^ 5.0 5.1 11.12. Great Dodecahemidodecahedron, Great Icosidodecahedron, Great Icosihemidodecahedron . 3d-meier.de. [2021-09-06 ] . пјҲеҺҹе§ӢеҶ…е®№ еӯҳжЎЈдәҺ2021-09-06пјү. ^ Jean Paul Albert Badoureau. MГ©moire sur les Figures IsocГЁles. Journal de l'Гүcole polytechnique. 1881, (49): 47-172. ^ Zvi Har'El. Kaleido Data: Uniform Polyhedron #75, great dodecahemidodecahedron . 2006-11-14 [2021-09-06 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2009-01-07пјү. ^ 8.0 8.1 Barnes, John. Shapes and Solids. Gems of Geometry (Springer). 2012: 27вҖ“62. ^ Perry Iv, John J and Perman, Jason A and Zaworotko, Michael J. Design and synthesis of metal--organic frameworks using metal-organic polyhedra as supermolecular building blocks . Chemical Society Reviews (Royal Society of Chemistry). 2009, 38 (5): 1400вҖ“1417. ^ Roman E. Maeder. 70: great dodecahemidodecahedron . mathconsult.ch. MathConsult AG. 1997 [2021-09-06 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2020-02-17пјү. ^ 11.0 11.1 11.2 Data of Great Dodecahemidodecahedron . dmccooey.com. [2018-10-17 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2017-10-03пјү. ^ Data of Great Icosidodecahedron . dmccooey.com. [2018-10-17 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2018-05-01пјү. ^ David I. McCooey. Versi-Regular Polyhedra: Great Dodecahemidodecahedron . dmccooey.com. [2021-09-05 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2019-10-03пјү. ^ GГ©vay, GГЎbor,. Constructions for large spatial point-line (nk) congurations. ARS Mathematica Contemporanea. 2013, 7 (1): 175вҖ“199. ^ 15.0 15.1 Uniform polyhedra . Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1954-05-13, 246 (916): 401вҖ“450 [2021-09-06 ] . ISSN 0080-4614 doi:10.1098/rsta.1954.0003 еӯҳжЎЈ дәҺ2020-09-18пјү пјҲиӢұиҜӯпјү . ^ Gorini, Catherine A., Geometry at Work , MAA Notes 53 , Cambridge University Press: 181, 2000, ISBN 9780883851647 ^ McMullen, Peter. Rigidity of Regular Polytopes. Rigidity and Symmetry (Springer). 2014: 253вҖ“вҖ“278. ^ Stellation of Regular Maps . Regular Map database - map details, weddslist.com. [2021-09-06 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2021-08-23пјү. ^ N14.3' . Regular Map database - map details, weddslist.com. [2021-07-30 ] . пјҲеҺҹе§ӢеҶ…е®№ еӯҳжЎЈдәҺ2021-08-05пјү. ^ McMullen, P., Schulte, E. Regular Polytopes in Ordinary Space . Discrete & Computational Geometry. 1997/06/01, 17 (4): pp.449-478 [2021-09-06 ] . ISSN 1432-0444 doi:10.1007/PL00009304 еӯҳжЎЈ дәҺ2018-06-03пјү.
еӣӣйқўй«”зҫӨе°ҚзЁұ е…«йқўй«”зҫӨе°ҚзЁұ дәҢеҚҒйқўй«”зҫӨе°ҚзЁұ е…¶д»–













![жҲӘеҚҠдәҢеҚҒйқўдҪ“пјҲеҮёеҢ…пјү[5]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/02/Icosidodecahedron.png/250px-Icosidodecahedron.png)




![{\displaystyle {\ce {<->[\pi]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8deea10ebe9c2b65f039af2e77ae19399fa9a1ee)


![{\displaystyle {\ce {<->[\delta]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59bb43307cba9af023529bb69e0c25987ad28eab)











![{\displaystyle {\ce {<->[\varphi]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c4c8fd58f0cd67b79e8ad39572c6b127e2d2149)













