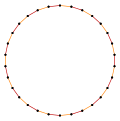
Пятнадцатиугольник

Пятнадцатиугольник
Правильный пятнандцатиугольник
Тип	Правильный многоугольник
Рёбра	15
Символ Шлефли	{15}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D15)
Внутренний угол	156°
Свойства
выпуклый, вписанный, Равносторонний, равноугольный[англ.], изотоксальный
Медиафайлы на Викискладе

Пятнадцатиугольник — многоугольник с пятнадцатью сторонами.

Правильный пятнадцатиугольник представлен символом Шлефли {15}.

Правильный пятнадцатиугольник имеет внутренние углы 156°. Со стороной a пятнадцатиугольник имеет площадь, задаваемую формулой

${\displaystyle {\begin{aligned}A={\frac {15}{4}}a^{2}\mathrm {ctg} \,{\frac {\pi }{15}}&={\frac {15}{4}}{\sqrt {7+2{\sqrt {5}}+2{\sqrt {15+6{\sqrt {5}}}}}}a^{2}\\&={\frac {15a^{2}}{8}}\left({\sqrt {3}}+{\sqrt {15}}+{\sqrt {2}}{\sqrt {5+{\sqrt {5}}}}\right)\\&\simeq 17.642362910544204\,a^{2}.\end{aligned}}}$

Правильный треугольник, десятиугольник и пятнадцатиугольник могут полностью закрыть вершину на плоскости.

Поскольку 15 = 3 × 5 является произведением различных простых чисел Ферма, правильный пятнадцатиугольник можно построить с помощью циркуля и линейки: Следующие построения правильного пятнадцатиугольника с заданной описывающей окружностью аналогично иллюстрации для утверждения XVI в книге IV Начал Евклида^[1].

Сравнение построения с построением Евклида см. на рисунке Пятнадцатиугольник

В построении для заданной описывающей окружности: ${\displaystyle {\overline {FG}}={\overline {CF}}{\text{,}}\;{\overline {AH}}={\overline {GM}}{\text{,}}\;|E_{1}E_{6}|}$ равна стороне равностороннего треугольника, а ${\displaystyle |E_{2}E_{5}|}$ равна стороне правильного пятиугольника^[2]. Точка ${\displaystyle H}$ делит радиус ${\displaystyle {\overline {AM}}}$ в пропорции золотого сечения: ${\displaystyle {\frac {\overline {AH}}{\overline {HM}}}={\frac {\overline {AM}}{\overline {AH}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1,618{\text{.}}}$

Сравнение с первой анимацией (с зелёными прямыми) приведено на следующих двух рисунках. Две дуги (для углов 36° и 24°) смещены против часовой стрелки. Построение не использует отрезок ${\displaystyle {\overline {CG}}}$, а вместо него использует отрезок ${\displaystyle {\overline {MG}}}$ как радиус ${\displaystyle {\overline {AH}}}$ для второй дуги (угол 36°).

Построение с помощью циркуля и линейки для заданной длины стороны. Построение почти такое же, что и для построения пятиугольника по заданной стороне, оно также начинается с создания отрезка как продолжения стороны, здесь ${\displaystyle {\overline {FE_{2}}}{\text{,}}}$, который делится в пропорции золотого сечения:

${\displaystyle {\frac {\overline {E_{1}E_{2}}}{\overline {E_{1}F}}}={\frac {\overline {E_{2}F}}{\overline {E_{1}E_{2}}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618033988749895{\text{.}}}$

Радиус описанной окружности ${\displaystyle {\overline {E_{2}M}}=R\;;\;\;}$

Длина стороны ${\displaystyle {\overline {E_{1}E_{2}}}=a\;;\;\;}$

Угол ${\displaystyle DE_{1}M=ME_{2}D=78^{\circ }}$

${\displaystyle {\begin{aligned}R&=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)={\frac {1}{2}}\cdot {\sqrt {8+2\cdot {\sqrt {5}}+2{\sqrt {15+6\cdot {\sqrt {5}}}}}}\cdot a\\&={\frac {\sin(78^{\circ })}{\sin(24^{\circ })}}\cdot a\approx 2.4048671723720654\cdot a\end{aligned}}}$

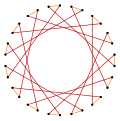
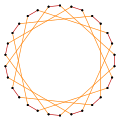
Правильный пятнадцатиугольник имеет диэдральную симметрию порядка 30 (Dih₁₅), представленную 15 прямыми зеркального отражения. Dih₁₅ имеет 3 диэдральные подгруппы: Dih₅, Dih₃ и Dih₁. А кроме того, ещё четыре циклические симметрии — Z₁₅, Z₅, Z₃ и Z₁, где Z_n представляет π/n вращательную симметрию.

В пятнадцатиугольнике имеется 8 различных симметрий. Джон Конвей обозначил симметрии буквами с указанием порядка симметрии после буквы^[3]. Он обозначил через r30 полную симметрию отражений Dih₁₅, обозначил через d (diagonal = диагональ) отражения относительно прямых, проходящих через вершины, через p отражения относительно прямых, проходящих через середины рёбер (perpendicular = перпендикуляр), а для пятнадцатиугольника с нечётным числом вершин использовал букву i (для зеркал через вершину и середину ребра) и букву g для циклической симметрии. Символ a1 означает отсутствие симметрии.

Эти низкие степени симметрий определяют степени свободы в определении неправильных пятнадцатиугольников. Только подгруппа g15 не имеет степеней свободы, но может рассматриваться как обладающая ориентированными рёбрами.

Существует три правильных звезды: {15/2}, {15/4}, {15/7} на тех же самых 15 вершинах правильного пятнадцатиугольника, но соединённых через одну, через три или через шесть вершин.

Есть также три правильных звёздчатых фигуры^[англ.]: {15/3}, {15/5}, {15/6}, первая состоит из трёх пятиугольников, вторая состоит из пяти правильных треугольников, а третья состоит из трёх пентаграмм.

Составную фигуру {15/3} можно рассматривать как двухмерный эквивалент трёхмерного соединения пяти тетраэдров.

Picture	{15/2}	{15/3} or 3{5}	{15/4}	{15/5} or 5{3}	{15/6} or 3{5/2}	{15/7}
Внутренний угол[англ.]	132°	108°	84°	60°	36°	12°

Более глубокие усечения правильного пятнадцатиугольника и пентадекаграмм могут дать изогональные (вершинно транзитивные) промежуточные звёздчатые многоугольники, образованные вершинами, находящимися на одинаковом расстоянии, и двумя длинами рёбер^[4].

Вершинно транзитивные функции на пятнадцатиугольнике
Квазирегулярные	Равноугольные							Квазирегулярные
t{15/2}={30/2}								t{15/13}={30/13}
t{15/7} = {30/7}								t{15/8}={30/8}
t{15/11}={30/22}								t{15/4}={30/4}

Правильный пятнадцатиугольник является многоугольником Петри для некоторого многогранника высокой размерности, полученного ортогональной проекцией:

14-симплекс (14D)

Он также является многоугольником Петри для большого 120-ячейника^[англ.] и великого звёздчатого 120-ячейника^[англ.].

• Weisstein, Eric W. Pentadecagon (англ.) на сайте Wolfram MathWorld.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии. Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником.