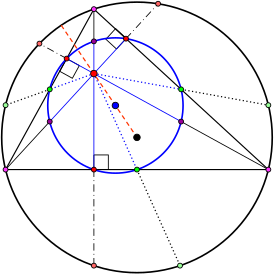
–¶–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ –¶–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ –Ę—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–į—Ź –≤–ĺ–ļ—Ä—É–≥ –Ĺ–Ķ–≥–ĺ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć (—á–Ķ—Ä–Ĺ–į—Ź) –ł –Ķ—Ď —Ü–Ķ–Ĺ—ā—Ä (—á—Ď—Ä–Ĺ—č–Ļ), –≤—č—Ā–ĺ—ā—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į (—á–į—Ā—ā—Ć –≤—č—Ā–ĺ—ā—č, —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–į—Ź –≤–Ĺ—É—ā—Ä–ł –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –≠–Ļ–Ľ–Ķ—Ä–į, —Ā–ł–Ĺ—Ź—Ź, –į –≤–Ĺ–Ķ - –Ķ—Ď —á–Ķ—Ä–Ĺ–į—Ź) –ł –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ (—Ā–ł–Ĺ—Ź—Ź) –ł –Ķ—Ď —Ü–Ķ–Ĺ—ā—Ä (—Ā–ł–Ĺ–ł–Ļ)
–Ď–į—Ä–ł—Ü–Ķ–Ĺ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č
a
2
(
b
2
+
c
2
)
‚ąí
(
b
2
‚ąí
c
2
)
2
:
{\displaystyle a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}:}
b
2
(
c
2
+
a
2
)
‚ąí
(
c
2
‚ąí
a
2
)
2
:
{\displaystyle b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}:}
c
2
(
a
2
+
b
2
)
‚ąí
(
a
2
‚ąí
b
2
)
2
{\displaystyle c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}}
–Ę—Ä–ł–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ—č–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č
cos
‚Ā°
(
B
‚ąí
C
)
:
cos
‚Ā°
(
C
‚ąí
A
)
:
cos
‚Ā°
(
A
‚ąí
B
)
{\displaystyle \cos(B-C):\cos(C-A):\cos(A-B)}
–ö–ĺ–ī –≠–¶–Ę
X(5)
–ė–∑–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ–į—Ź
—ā–ĺ—á–ļ–į –ö–ĺ—Ā–Ĺ–ł—ā—č
–¶–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ ‚ÄĒ –ĺ–ī–Ĺ–į –ł–∑ –∑–į–ľ–Ķ—á–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į . –ē—Ď —á–į—Ā—ā–ĺ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—ā –ļ–į–ļ
O
9
{\displaystyle O_{9}}
–ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ , –ł–Ľ–ł –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –≠–Ļ–Ľ–Ķ—Ä–į, –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ –ī–Ķ–≤—Ź—ā—Ć –≤–į–∂–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č —Ā—ā–ĺ—Ä–ĺ–Ĺ, –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź —ā—Ä—Ď—Ö –≤—č—Ā–ĺ—ā –ł —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤, —Ā–ĺ–Ķ–ī–ł–Ĺ—Ź—é—Č–ł—Ö –ĺ—Ä—ā–ĺ—Ü–Ķ–Ĺ—ā—Ä —Ā –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į. –¶–Ķ–Ĺ—ā—Ä —ć—ā–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —É–ļ–į–∑–į–Ĺ –ļ–į–ļ —ā–ĺ—á–ļ–į X(5) –≤ —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł–ł —Ü–Ķ–Ĺ—ā—Ä–ĺ–≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ö–Ľ–į—Ä–ļ–į –ö–ł–ľ–Ī–Ķ—Ä–Ľ–ł–Ĺ–≥–į [ 1] [ 2]
O
9
O
=
O
9
H
=
3
O
9
M
.
{\displaystyle O_{9}O=O_{9}H=3O_{9}M~.}
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ķ—Ā–Ľ–ł –Ņ–į—Ä–į –ł–∑ —ć—ā–ł—Ö —á–Ķ—ā—č—Ä—Ď—Ö —Ü–Ķ–Ĺ—ā—Ä–ĺ–≤ –ł–∑–≤–Ķ—Ā—ā–Ĺ–į, –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ī–≤—É—Ö –ī—Ä—É–≥–ł—Ö –Ľ–Ķ–≥–ļ–ĺ –Ĺ–į–Ļ—ā–ł.
–ź–Ĺ–ī—Ä—é –ď–ł–Ĺ–į–Ĺ–ī (Andrew Guinand) –≤ 1984-–ľ –≥–ĺ–ī—É, –ł—Ā—Ā–Ľ–Ķ–ī—É—Ź –∑–į–ī–į—á—É, –Ĺ—č–Ĺ–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ—É—é –ļ–į–ļ –∑–į–ī–į—á–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –≠–Ļ–Ľ–Ķ—Ä–į , –Ņ–ĺ–ļ–į–∑–į–Ľ, —á—ā–ĺ –Ķ—Ā–Ľ–ł –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ —ć—ā–ł—Ö —Ü–Ķ–Ĺ—ā—Ä–ĺ–≤ –ī–Ľ—Ź –Ĺ–Ķ–ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –∑–į–ī–į–Ĺ–ĺ, —ā–ĺ –ł–Ĺ—Ü–Ķ–Ĺ—ā—Ä —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ľ–Ķ–∂–ł—ā –≤–Ĺ—É—ā—Ä–ł –ĺ—Ä—ā–ĺ—Ü–Ķ–Ĺ—ā—Ä–ĺ–ł–ī–į–Ľ—Ć–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł [–į–Ĺ–≥–Ľ.] [ 4] [ 5] [ 6] [ 7]
–†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —Ü–Ķ–Ĺ—ā—Ä–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ –ī–ĺ –ł–Ĺ—Ü–Ķ–Ĺ—ā—Ä–į
I
{\displaystyle I}
I
O
9
<
1
2
I
O
,
{\displaystyle IO_{9}<{\dfrac {1}{2}}IO~,}
I
O
9
=
1
2
(
R
‚ąí
2
r
)
<
R
2
,
{\displaystyle IO_{9}={\dfrac {1}{2}}(R-2r)<{\frac {R}{2}}~,}
2
R
‚čÖ
I
O
9
=
O
I
2
,
{\displaystyle 2R\cdot IO_{9}=OI^{2}~,}
–≥–ī–Ķ
R
{\displaystyle R}
r
{\displaystyle r}
–ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ł –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ.
–¶–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ—č—Ö –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į , –ĺ—Ä—ā–ĺ—ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –≠–Ļ–Ľ–Ķ—Ä–į[ 8] [ 3]
–¶–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ł–ī–ĺ–ľ —á–Ķ—ā—č—Ä—Ď—Ö —ā–ĺ—á–Ķ–ļ ‚ÄĒ —ā—Ä—Ď—Ö —ā–ĺ—á–Ķ–ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ł –Ķ–≥–ĺ –ĺ—Ä—ā–ĺ—Ü–Ķ–Ĺ—ā—Ä–į [ 9]
–ė–∑ –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ –Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –≠–Ļ–Ľ–Ķ—Ä–į —ā—Ä–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į–ľ–ł –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤, —Ā–ĺ–Ķ–ī–ł–Ĺ—Ź—é—Č–ł—Ö –≤–Ķ—Ä—ą–ł–Ĺ—č —Ā –ĺ—Ä—ā–ĺ—Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ (–≤–Ķ—Ä—ą–ł–Ĺ—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –≠–Ļ–Ľ–Ķ—Ä–į-–§–Ķ–Ļ–Ķ—Ä–Ī–į—Ö–į). –≠—ā–ł —ā—Ä–ł —ā–ĺ—á–ļ–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł—Ź–ľ–ł —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ü–Ķ–Ĺ—ā—Ä–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ.
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ —Ā–Ľ—É–∂–ł—ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł , –Ņ–Ķ—Ä–Ķ–≤–ĺ–ī—Ź—Č–ł–ľ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–Ĺ—č–Ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –≠–Ļ–Ľ–Ķ—Ä–į-–§–Ķ–Ļ–Ķ—Ä–Ī–į—Ö–į (–ł –Ĺ–į–ĺ–Ī–ĺ—Ä–ĺ—ā) [ 3]
–°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –õ–Ķ—Ā—ā–Ķ—Ä–į —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ –Ľ–Ķ–∂–ł—ā –Ĺ–į –ĺ–ī–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —ā—Ä–Ķ–ľ—Ź –ī—Ä—É–≥–ł–ľ–ł —ā–ĺ—á–ļ–į–ľ–ł ‚ÄĒ –ī–≤—É–ľ—Ź —ā–ĺ—á–ļ–į–ľ–ł –§–Ķ—Ä–ľ–į –ł —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł [ 10] –Ę–ĺ—á–ļ–į –ö–ĺ—Ā–Ĺ–ł—ā–į , –ł–∑–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ–į—Ź —Ü–Ķ–Ĺ—ā—Ä—É –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ
–Ę—Ä–ł–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ—č–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ü–Ķ–Ĺ—ā—Ä–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–Ķ–≤—Ź—ā–ł —ā–ĺ—á–Ķ–ļ —Ä–į–≤–Ĺ—č[ 1] [ 2]
cos
‚Ā°
(
B
‚ąí
C
)
:
cos
‚Ā°
(
C
‚ąí
A
)
:
cos
‚Ā°
(
A
‚ąí
B
)
{\displaystyle \cos(B-C):\cos(C-A):\cos(A-B)}
=
cos
‚Ā°
A
+
2
cos
‚Ā°
B
cos
‚Ā°
C
:
cos
‚Ā°
B
+
2
cos
‚Ā°
C
cos
‚Ā°
A
:
cos
‚Ā°
C
+
2
cos
‚Ā°
A
cos
‚Ā°
B
{\displaystyle =\cos A+2\cos B\cos C:\cos B+2\cos C\cos A:\cos C+2\cos A\cos B}
=
cos
‚Ā°
A
‚ąí
2
sin
‚Ā°
B
sin
‚Ā°
C
:
cos
‚Ā°
B
‚ąí
2
sin
‚Ā°
C
sin
‚Ā°
A
:
cos
‚Ā°
C
‚ąí
2
sin
‚Ā°
A
sin
‚Ā°
B
{\displaystyle =\cos A-2\sin B\sin C:\cos B-2\sin C\sin A:\cos C-2\sin A\sin B}
=
b
c
[
a
2
(
b
2
+
c
2
)
‚ąí
(
b
2
‚ąí
c
2
)
2
]
:
c
a
[
b
2
(
c
2
+
a
2
)
‚ąí
(
c
2
‚ąí
a
2
)
2
]
:
a
b
[
c
2
(
a
2
+
b
2
)
‚ąí
(
a
2
‚ąí
b
2
)
2
]
.
{\displaystyle =bc[a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}]:ca[b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}]:ab[c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}]~.}
–Ď–į—Ä–ł—Ü–Ķ–Ĺ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ü–Ķ–Ĺ—ā—Ä–į —Ä–į–≤–Ĺ—č[ 2]
a
cos
‚Ā°
(
B
‚ąí
C
)
:
b
cos
‚Ā°
(
C
‚ąí
A
)
:
c
cos
‚Ā°
(
A
‚ąí
B
)
{\displaystyle a\cos(B-C):b\cos(C-A):c\cos(A-B)}
=
a
2
(
b
2
+
c
2
)
‚ąí
(
b
2
‚ąí
c
2
)
2
:
b
2
(
c
2
+
a
2
)
‚ąí
(
c
2
‚ąí
a
2
)
2
:
c
2
(
a
2
+
b
2
)
‚ąí
(
a
2
‚ąí
b
2
)
2
.
{\displaystyle =a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}:b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}:c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}~.}
‚ÜĎ 1 2 Kimberling, 1994 , —Ā. 163‚Äď187.‚ÜĎ 1 2 3 4 Encyclopedia of Triangle Centers –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 24 –Ĺ–ĺ—Ź–Ī—Ä—Ź 2015 –Ĺ–į Wayback Machine , accessed 2014-10-23.‚ÜĎ 1 2 3 Dekov, 2007 .‚ÜĎ Stern, 2007 , —Ā. 1‚Äď9.‚ÜĎ Euler, 1767 , —Ā. 103‚Äď123.‚ÜĎ Guinand, 1984 , —Ā. 290‚Äď300.‚ÜĎ Franzsen, 2011 , —Ā. 231‚ÄĒ236.‚ÜĎ –ó–ī–Ķ—Ā—Ć –Ĺ–Ķ —Ā–Ľ–Ķ–ī—É–Ķ—ā –Ņ—É—ā–į—ā—Ć —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –≠–Ļ–Ľ–Ķ—Ä–į –ł–∑ —ā–Ķ–ĺ—Ä–ł–ł —á–ł—Ā–Ķ–Ľ (–Ĺ–į–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ü–į—Ā–ļ–į–Ľ—Ź) –ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –≠–Ļ–Ľ–Ķ—Ä–į –ļ–į–ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ, –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–Ĺ—č–Ļ —ā–ĺ—á–ļ–į–ľ–ł –≠–Ļ–Ľ–Ķ—Ä–į. –Ę–ĺ—á–ļ–ł –≠–Ļ–Ľ–Ķ—Ä–į ‚ÄĒ —ć—ā–ĺ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č –ĺ—ā—Ä–Ķ–∑–ļ–ĺ–≤, —Ā–ĺ–Ķ–ī–ł–Ĺ—Ź—é—Č–ł—Ö –ĺ—Ä–ĺ—ā–ĺ—Ü–Ķ–Ĺ—ā—Ä —Ā –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į.
‚ÜĎ –≠–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź —Ü–Ķ–Ĺ—ā—Ä–ĺ–≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ņ—Ä–ł–Ņ–ł—Ā—č–≤–į–Ķ—ā —ć—ā–ĺ –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–Ķ –†—ć–Ĺ–ī–ł –•—Ć—é—Ā—ā–ĺ–Ĺ—É(Randy Hutson, 2011).
‚ÜĎ Yiu, 2010 , —Ā. 175‚Äď209.‚ÜĎ Rigby, 1997 , —Ā. 156‚Äď158.
Kimberling. Central Points and Central Lines in the Plane of a Triangle // Mathematics Magazine. ‚ÄĒ 1994. ‚ÄĒ –Ę. 67 , –≤—č–Ņ. 3 . ‚ÄĒ JSTOR 2690608 Stern. Euler‚Äôs triangle determination problem // Forum Geometricorum. ‚ÄĒ 2007. ‚ÄĒ –Ę. 7 .Dekov. Nine-point center // Journal of Computer-Generated Euclidean Geometry. ‚ÄĒ 2007.Euler. Solutio facilis problematum quorundam geometricorum difficillimorum (Latin) // Novi Commentarii academiae scientiarum Petropolitanae. ‚ÄĒ 1767. ‚ÄĒ –Ę. 11 .Andrew P. Guinand. Euler lines, tritangent centers, and their triangles // American Mathematical Monthly . ‚ÄĒ 1984. ‚ÄĒ –Ę. 91 , –≤—č–Ņ. 5 . ‚ÄĒ JSTOR 2322671 William N. Franzsen. The distance from the incenter to the Euler line // Forum Geometricorum. ‚ÄĒ 2011. ‚ÄĒ –í—č–Ņ. 11 .Paul Yiu. The circles of Lester, Evans, Parry, and their generalizations // Forum Geometricorum. ‚ÄĒ 2010. ‚ÄĒ –Ę. 10 .Rigby. Brief notes on some forgotten geometrical theorems // Mathematics and Informatics Quarterly. ‚ÄĒ 1997. ‚ÄĒ Vol. 7.
–í–ł–ī—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ –ó–į–ľ–Ķ—á–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –Ľ–ł–Ĺ–ł–ł –ó–į–ľ–Ķ—á–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–ĺ—á–ļ–ł –ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –Ē–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ě–Ī–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź
–≠—ā–į —Ā—ā–į—ā—Ć—Ź –Ĺ—É–∂–ī–į–Ķ—ā—Ā—Ź –≤ –ī–ĺ—Ä–Ī–ĺ—ā–ļ–Ķ:






















![{\displaystyle =bc[a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}]:ca[b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}]:ab[c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}]~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0392caaa1bdfcf234f158eaccfc5c7373ae9a77b)















