Ромбоікосододекаедр

Ромбоікосододека́едр^[1][2][3] — напівправильний багатогранник, який складається з 12 правильних п'ятикутників, 30 квадратів і 20 трикутників, архімедове тіло. Має ікосаедричний тип симетрії. В кожній з вершин сходяться трикутник, п'ятикутник і 2 квадрати.

Ромбоікосододекаедр можна подати як додекаедр, зрізаний за вершинами і ребрами (при цьому трикутники відповідають вершинам додекаедра, а квадрати — ребрам), або як ікосаедр, зрізаний так само (при цьому п'ятикутники відповідають вершинам ікосаедра, а квадрати — ребрам), або ж як зрізаний ікосододекаедр, чим він по суті і є.

Декартові координати вершин ромбоікосододекаедра з довжиною ребра 2 із центром у початку координат є парними перестановками з:^[4]

(± 1, ± 1, ± φ ³),

(± φ ², ± φ, ± 2 φ),

(± (2+ φ), 0, ± φ ²), де φ = 1 + √5/2 являє собою золотий перетин . Отже, радіус описаної сфери цього ромбоікосододекаедра дорівнює відстані цих точок від початку координат, а саме √φ⁶+2 = √8φ+7 для довжини ребра 2. Для одиничної довжини ребра, зменшивши R удвічі, маємо

R = √8φ+7/2 = √11+4√5/2 ≈ 2,233.

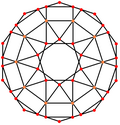
Ортогональна проєкція в Геометрії (1543) Августина Гіршфоґеля

Ромбоікосододекаедр має шість особливих ортогональних проєкцій, центрованих на вершині, на ребрах двох типів і гранях трьох типів: трикутнику, квадраті та п'ятикутнику. Останні дві відповідають площинам Коксетера А₂ і Н₂.

Ортогональні проєкції

У центрі	Вершина	Ребро 3-4	Ребро 5-4	Квадратна грань	Трикутна грань	П'ятикутна грань
Суцільна
Каркасна
Проєктивна симетрія	[2]	[2]	[2]	[2]	[6]	[10]
Дуальне зображення

Ромбоікосододекаедр також можна зобразити у вигляді сферичної мозаїки та проєктувати на площину за допомогою стереографічної проєкції . Ця проєкція є конформною, зберігаючи кути, але не площі та довжини. Прямі лінії на кулі проєктуються на площину як дуги кола.

	У центрі —п'ятикутник	У центрі — трикутник	У центрі — квадрат
Ортогональна проєкція	Стереографічні проєкції

Сімейство однорідних ікосаедричних багатогранників

Симетрія: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Двоїсті до однорідних багатогранників
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

• Ромбозрізаний ікосододекаедр

• М. Веннинджер. Модели многогранников. — Мир, 1974.
• Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М. : Государственное издательство физико-математической литературы, 1963. — С. 382-447.
• Л. А. Люстерник. Выпуклые фигуры и многогранники. — М. : Государственное издательство технико-теоретической литературы, 1956.