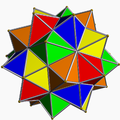
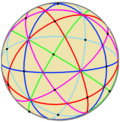
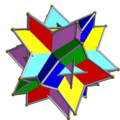
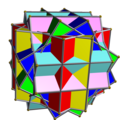
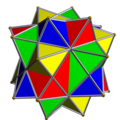
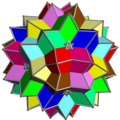
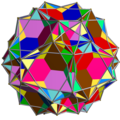
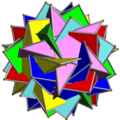
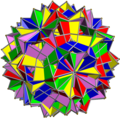
З'єднання многогранників

З'єднання многогранників — геометричне тіло, складене з деяких многогранників, що мають спільний центр. З'єднання є тривимірним аналогом багатокутних з'єднань, таких як гексаграма.

Зовнішні вершини з'єднання можна з'єднати, утворивши опуклий многогранник, який називають опуклою оболонкою. З'єднання є огрануванням опуклої оболонки.

Усередині з'єднання утворюється менший опуклий многогогранник, спільна частина всіх членів з'єднання. Його називають ядром набору зірчастих многогранників.

Правильне з'єднання многогранників можна визначити як з'єднання, яке, як і в разі правильних многогранників, є вершинно-транзитивним^[en], реберно-транзитивним та гране-транзитивним. Існує п'ять правильних з'єднань многогранників.

З'єднання	Малюнок	Сферичне подання	Опукла оболонка	Ядро	Симетрія	Підгрупа для одного складника	Двоїстий
Два тетраедри (зірчастий октаедр)			Куб	Октаедр	*432 [4,3] O h	*332 [3,3] T d	Самодвоїстий
П'ять тетраедрів			Додекаедр	Ікосаедр	532 [5,3] + I	332 [3,3] + T	Енантіоморфний хіральний двійник
Десять тетраедрів			Додекаедр	Ікосаедр	*532 [5,3] I h	332 [3,3] T	Самодвоїстий
П'ять кубів[en]			Додекаедр	Ромботриаконтаедр	*532 [5,3] I h	3*2 [3,3] T h	П'ять октаедрів
П'ять октаедрів[en]			Ікосододекаедр	Ікосаедр	*532 [5,3] I h	3*2 [3,3] T h	П'ять кубів

Найвідомішим є з'єднання двох тетраедрів. Кеплер назвав це з'єднання латиною stella octangula (зірчастий октаедр). Вершини двох тетраедрів задають куб, а їх перетин є октаедром, грані якого лежать на тих самих площинах, що й грані складових тетраедрів. Таким чином, з'єднання є зведенням до зірчастої форми октаедра і фактично його єдиним можливим зведенням.

Зірчастий октаедр можна також розглядати як двоїсто-правильне з'єднання.

З'єднання п'яти тетраедрів має дві дзеркальні версії, які разом дають з'єднання десяти тетраедрів. Всі з'єднання тетраедрів самодвоїсті, а з'єднання п'яти кубів двоїсте з'єднанню п'яти октаедрів.

Двоїсте з'єднання — це з'єднання многогранника і двоїстого йому, розташованих взаємно протилежно відносно спільної вписаної або напіввписаної сфери, так що ребро одного многогранника перетинає двоїсте ребро двоїстого многогранника. Існує п'ять таких з'єднань правильних многогранників.

Компоненти	Малюнок	Опукла оболонка	Ядро	Симетрія
Два тетраедри (зірчастий октаедр)		Куб	Октаедр	*432 [4,3] Oh
Куб і октаедр[en]		Ромбододекаедр	Кубооктаедр	*432 [4,3] Oh
додекаедр та ікосаедр[en]		Ромботріаконтаедр	Ікосододекаедр	*532 [5,3] Ih
великий ікосаедр і великий зірчастий додекаедр[en]		Додекаедр	Ікосододекаедр	*532 [5,3] Ih
малий зірчастий додекаедр і великий додекаедр[en]		Ікосаедр	Додекаедр	*532 [5,3] Ih

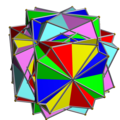
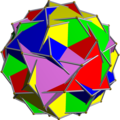
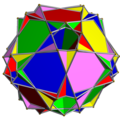
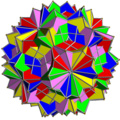
Тетраедр самодвоїстий, отже, двоїсте з'єднання тетраедра з двоїстим йому є також зірчастим октаедром.

Двоїсті з'єднання куб-октаедр та додекаедр-ікосаедр є ззірченнями кубооктаедра та ікосододекаедра відповідно.

З'єднання малого зірчастого додекаедра і великого додекаедра виглядає зовні як той самий малий зірчастий додекаедр, оскільки великий додекаедр міститься повністю всередині нього. Тому зображення малого зірчастого додекаедра, наведене вище, показано у вигляді реберного каркаса.

1976 року Джон Скіллінг (John Skilling) опублікував статтю Однорідні з'єднання однорідних многогранників^[1], у якій перерахував 75 з'єднань (серед них 6 нескінченних множин призматичних з'єднань, № 20-25), отриманих з однорідних многогранників за допомогою обертань. (Кожна вершина є вершинно-транзитивною^[en].) Список включає п'ять з'єднань правильних многогранників зі списку вище [1].

Ці 75 однорідних з'єднань наведено в таблиці нижче. У більшості з'єднань різні кольори відповідають різним складникам. Деякі хіральні пари розфарбовано згідно з дзеркальною симетрією.

• 1-19: суміш (4,5,6,9,17 є п'ятьма правильними з'єднаннями)

• 20-25: симетрія призм, вкладена в діедричну симетрію в тривимірному просторі^[en],

• 26-45: симетрія призм, укладена в октаедричну^[en] або ікосаедричну^[en] симетрію,

• 46-67: тетраедрична симетрія, вкладена в октаедричну або ікосаедричну симетрію,

• 68-75: енантіоморфні пари

З'єднання чотирьох кубів (ліворуч) не є ні правильним, ні двоїстим, ні однорідним з'єднанням. Двоїсте йому з'єднання чотирьох октаедрів (праворуч) однорідне.

• З'єднання трьох октаедрів^[en]
• З'єднання чотирьох кубів

Два многогранники, які є з'єднаннями, але їх елементи строго вкладені в малий складний ікосододекаедр^[en] (з'єднання ікосаедра та великого додекаедра) і великий складний ікосододекаедр^[en] (з'єднання малого зірчастого додекаедра і великого ікосаедра). Якщо прийняти узагальнене визначення однорідного багатогранника, вони будуть однорідними.

Розділ ентіаноморфних пар у списку Скіллінга не містить з'єднань двох великих кирпатих додекоікосододекаедрів^[en], оскільки грані- пентаграми збігаються. Видалення граней, що збігаються, приведе до з'єднання двадцяти октаедрів^[en].

Ортогональні проекції

75 {4,3,3}	75 {3,3,4}

У чотиривимірному просторі існує багато правильних з'єднань правильних політопів. Коксетер перерахував деякі з них у своїй книзі Правильні многогранники^[en][2].

Самодвоїсті:

Двоїсті пари:

Однорідні з'єднання з опуклими чотиривимірними многогранниками:

Двоїсті позиції:

Самодвоїсті зірчасті з'єднання:

Двоїсті пари з'єднань зірок:

Однорідні з'єднання зірок :

У термінах теорії груп, якщо G — група симетрії з'єднання многогранників і група діє транзитивно на многогранник (так що будь-який многогранник може перейти в будь-якій іншій, як в однорідних з'єднаннях), тоді, якщо H є стабілізатором одного вибраного многогранника, многогранники можна визначити за орбітою G/H.

Існує вісімнадцять двопараметричних сімейств правильних з'єднань мозаїк на евклідовій площині. У гіперболічному просторі відомі п'ять однопараметричних сімейств та сімнадцять ізольованих мозаїк, але список не завершено.

Евклідові та гіперболічні сімейства 2 {p,p} (4 ≤ p ≤ ∞, p ціле) аналогічні сферичним зірчастим октаедрам, 2 {3,3}.

Деякі приклади евклідових і гіперболічних правильних з'єднань

Самодвоїсті	Двоїсті		Самодвоїсті
2 {4,4}	2 {6,3}	2 {3,6}	2 {∞,∞}[en]
	3 {6,3}	3 {3,6}	3 {∞,∞}[en]

Відомим сімейством правильних евклідових з'єднань стільників у просторах розмірності п'ять і вище є нескінченне сімейство гіперкубічних стільників^[en], що мають спільні вершини та грані. Таке з'єднання може мати довільне число гіперкубічних стільників.

Існують також двоїсто-правильні з'єднання мозаїк. Простим прикладом є E²-з'єднання шестикутної мозаїки та її двоїстої трикутної. Евклідове з'єднання двох гіперкубічних стільників правильне і двоїсто правильне.

• MathWorld: Polyhedron Compound
• Compound polyhedra — від Virtual Reality Polyhedra
  • Uniform Compounds of Uniform Polyhedra
• Skilling's 75 Uniform Compounds of Uniform Polyhedra
• Skilling's Uniform Compounds of Uniform Polyhedra
• Polyhedral Compounds
• http://users.skynet.be/polyhedra.fleurent/Compounds_2/Compounds_2.htm
• Compound of Small Stellated Dodecahedron and Great Dodecahedron {5/2,5}+{5,5/2}