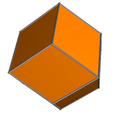
在幾何學 中,倒角立方體 又稱切稜立方体 或裁邊立方體 (英語:Chamfered Cube )是一種凸 十八面體 ,共有18 個面 、48 個邊 和32 個頂點 [ 1] 四角化截半立方體 的對偶多面體 ,是由立方體 經過倒角變換所產生的多面體 ,是一種方富勒烯 [ 3]
倒角立方體具有偶數邊數的面且180度旋轉對稱的邊,因此可以算作一種環帶多面體 ,也是一個從立方體不使用膨脹變換構造的一個環帶多面體 之一[ 4] 正方形 和六邊形 的面組成,因此也屬於一種八面體對稱的[ 5] 戈德堡多面體 ,符號為GIV (0,2)。此外由於倒角立方體擁有接近正多邊形 的面,且有很多面都是正多邊形(六個正方形 ),因此也是一種擬詹森多面體 。
倒角立方體具有18個面 、48個邊 和32個頂點 ,由6 個正方形 和12 六邊形 組成[ 2] 菱形十二面體 ,共截去了6個頂點,原本的十二個菱形變為十二個六邊形,截去的頂點變為六個正方形。
由於六邊形是因為切割而產生的,因此是全等 ,每個邊皆等邊,但不是正六邊形 ,兩個內角的角度跟原來的菱形十二面體 相同,為arccos (-1/3),約109.47度,而新截出來的四個內角約為125.26度,而正六邊形 內角是120度[ 6]
另外一種構造出倒角立方體的方式是由正方體 出發,將原本的面擴張,原本的角倒過來,剩下的空隙用六邊形填滿
此外,也可以看作是一種截邊的立方體,即將立方體的十二條邊切去[ 7]
倒角立方體可以視為切去所有四階頂點 的菱形十二面體 ,即切去切去相鄰四個面的頂點 ,因此也稱為截四階角菱形十二面體 ,有時會簡稱為截角菱形十二面體 [ 8] [ 9]
另外,倒角立方體也可以視為經過交錯截角 的菱形十二面體 ,即交錯地切除菱形十二面體 的頂點,但不是完全切除,因為完全切除會導致原有的菱形 面退化成二邊形 ,即退化為邊,造成結果變為立方體 ,因此,倒角立方體也可以稱為交錯截角菱形十二面體,同樣,這稱呼存在歧義,因為也可能是指倒角八面體[ 9] 交錯 的扭稜立方體 ,其結果僅是兩種手性 鏡像 ,而此例中的結果是倒角八面體以及倒角立方體。
倒角立方體是菱形十二面體 的閔可夫斯基和 [ 10]
(
±
1
,
±
1
,
±
1
)
{\displaystyle (\pm 1,\pm 1,\pm 1)}
(
±
2
,
0
,
0
)
{\displaystyle (\pm 2,0,0)}
邊長為a的倒角立方體,其體積 為:
V
=
a
3
×
(
8
+
40
3
9
+
19
+
8
3
3
)
≈
19.0074
a
3
{\displaystyle V=a^{3}\times {\biggr (}8+{\frac {40{\sqrt {3}}}{9}}+{\sqrt {\frac {19+8{\sqrt {3}}}{3}}}{\biggr )}\approx 19.0074a^{3}}
表面積 為:
A
=
a
2
×
(
6
+
8
2
(
1
+
3
)
)
≈
36.9096
a
2
{\displaystyle A=a^{2}\times {\biggr (}6+8{\sqrt {2}}(1+{\sqrt {3}}){\biggr )}\approx 36.9096a^{2}}
正方形 面的內切球 半徑 為:
r
4
=
a
×
19
2
+
4
3
6
≈
1.6547
a
{\displaystyle r_{4}=a\times {\sqrt {\frac {{\frac {19}{2}}+4{\sqrt {3}}}{6}}}\approx 1.6547a}
六邊形 面的內切球 半徑為:
r
6
=
a
×
(
8
3
+
2
2
)
≈
1.5236
a
{\displaystyle r_{6}=a\times {\biggr (}{\frac {{\sqrt {\frac {8}{3}}}+{\sqrt {2}}}{2}}{\biggr )}\approx 1.5236a}
倒角倒角立方體或二次倒角立方體,即進行兩次倒角的立方體,亦可以稱為倒角交錯截角菱形十二面體。
下表列出立方體倒角四次以下的多面體。藍色代表來自於正方體的面、綠色代表經過一次倒角後產生的面、紅色是兩次、紫色是三次、黃色是四次。前幾個的面數是6, 18, 66, 258, 1026, 4098,...... (OEIS 數列A178789 )、邊數是12, 48, 192, 768, 3072, 12288,...... (OEIS 數列A164346 )、頂點數是2, 8, 32, 128, 512, 2048, 8192,...... (OEIS 數列A004171 )。其頂點數皆為二次冪 ,因此對偶多面體也是2n 面體。此外,這些多面體全部都是戈德堡多面體 [ 11]
倒角立方体有一個對稱性為五角十二面體 群的拓樸同構體,其可以透過截去五角十二面體中與座標軸平行的棱構造。這種立體為黃鐵礦的晶形之一。
這種立體也可以視為特殊的切稜立方體,其可以透過切角小於45度且深度大於零的方式切去立方體的稜來構造[ 12]
利用24個倒角立方體堆砌出的截角八面體 模型 倒角立方體與截角八面體 十分類似。
倒角立方體
截角八面體
可以利用24個倒角立方體堆砌出一個截角八面體 的模型[ 13] [ 14]
倒角立方體是立方體透過一種截邊的變換產生的,截邊也可以產生一些不同的多面體,例如:
倒角立方體是一種正多面體倒角變換結果,其他正多面體或卡塔蘭立體 也可以透過倒角變換得到一系列的多面體:
倒角立方體也是一種多邊形-六邊形鑲嵌。
^ 1.0 1.1 Chamfered Cube Data (页面存档备份 ,存于互联网档案馆 ) dmccooey.com [2016-1-17]^ 2.0 2.1 Sie-Chin Tjong. Nanocrystalline Materials: Their Synthesis-Structure-Property Relationships and Applications . Elsevier. 2006: 117 . ISBN 9780080479606 ISBN 008047960X [2016-1-17]^ Deza, A.; Deza, M. ; Grishukhin, V., Fullerenes and coordination polyhedra versus half-cube embeddings , Discrete Mathematics 192 (1): 41–80 [2013-03-18 ] , doi:10.1016/S0012-365X(98)00065-X 原始内容 存档于2007-02-06) ^ 0xDE(11011110) Zonohedra and cubic partial cubes (页面存档备份 ,存于互联网档案馆 ) 11011110.livejournal.com 2005-9-6 [2016-1-7]
^ Clinton’s Equal Central Angle Conjecture, JOSEPH D. CLINTON
^ V.A. Zalgaller Convex polyhedra with regular faces Seminar in Mathematics of V. A. Steklov Math. Institute, Leningrad 2 Consultants Bureau, New York (1969)
^ chamferedcube (页面存档备份 ,存于互联网档案馆 ) matematicasvisuales.com [2016-1-17]^ Eppstein, David . The Geometry Junkyard: Zonohedra and Zonotopes . [2016-01-16 ] . (原始内容存档 于2020-03-16). ^ 9.0 9.1 a truncated form of the rhombic dodecahedron (页面存档备份 ,存于互联网档案馆 ) robertlovespi.net 2014-6-9 [2016-1-17]^ Hazewinkel, Michiel (编), Minkowski addition , 数学百科全书 , 施普林格科学+商业媒体 , 2001, ISBN 978-1-55608-010-4 [失效連結 ^ Hart, George . Goldberg Polyhedra. Senechal, Marjorie (编). Shaping Space 2nd. Springer. 2012: 125–138. doi:10.1007/978-0-387-92714-5_9 ^ 多面体木工. 特定非営利活動法人 科学協力学際センター. 2006-08-01. ^ Gallery of Wooden Polyhedra (页面存档备份 ,存于互联网档案馆 ) woodenpolyhedra.web.fc2.com^ "Wooden polyhedra(English edition)" (页面存档备份 ,存于互联网档案馆 ) woodenpolyhedra.web.fc2.com