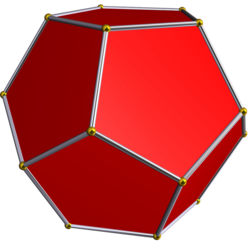
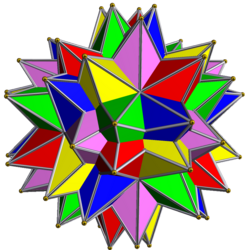
–ú–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä
–ú–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä [3] [1][4] ‚ÄĒ –ĺ–ī–ł–Ĺ –∑ —á–ĺ—ā–ł—Ä—Ć–ĺ—Ö –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ł—Ö –∑—Ė—Ä—á–į—Ā—ā–ł—Ö –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ—Ė–≤ –ö–Ķ–Ņ–Ľ–Ķ—Ä–į ‚ÄĒ –ü—É–į–Ĺ—Ā–ĺ. –ú–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į—ć–ī—Ä –≤–Ņ–Ķ—Ä—ą–Ķ –Ņ–ĺ–≤–Ĺ—Ė—Ā—ā—é –ĺ–Ņ–ł—Ā–į–Ĺ–ĺ –≤ —ā—Ä–į–ļ—ā–į—ā—Ė –ô–ĺ–≥–į–Ĺ–Ĺ–į –ö–Ķ–Ņ–Ľ–Ķ—Ä–į 1619 —Ä–ĺ–ļ—É ¬ęHarmonices Mundi¬Ľ[5][6], –į –Ĺ–į–∑–≤—É –Ļ–ĺ–ľ—É –ī–į–≤ –ź—Ä—ā—É—Ä –ö–Ķ–Ļ–Ľ—Ė –≤ 1859 —Ä–ĺ—Ü—Ė. [1] –ü–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź:
–ú–į—Ē 12 –≥—Ä–į–Ĺ–Ķ–Ļ ‚ÄĒ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ł—Ö –Ņ'—Ź—ā–ł–Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ–≤–ł—Ö –∑—Ė—Ä–ĺ–ļ (–Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ), —Ź–ļ—Ė –Ņ–Ķ—Ä–Ķ—ā–ł–Ĺ–į—é—ā—Ć—Ā—Ź –ľ—Ė–∂ —Ā–ĺ–Ī–ĺ—é —ā–į 12 –≤–Ķ—Ä—ą–ł–Ĺ. –®—Ė—Ā—ā—Ć –Ņ–į—Ä –≥—Ä–į–Ĺ–Ķ–Ļ –Ľ–Ķ–∂–į—ā—Ć –≤ –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł—Ö –Ņ–Ľ–ĺ—Č–ł–Ĺ–į—Ö. –ô–ĺ–≥–ĺ —Ā–ł–ľ–≤–ĺ–Ľ –®–Ľ–Ķ—Ą–Ľ—Ė ‚ÄĒ . –¶–Ķ –ĺ–∑–Ĺ–į—á–į—Ē, —Č–ĺ –ļ–ĺ–∂–Ĺ–į –≤–Ķ—Ä—ą–ł–Ĺ–į –ĺ—ā–ĺ—á–Ķ–Ĺ–į 5-–ľ–į –≥—Ä–į–Ĺ—Ź–ľ–ł (–Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ–į–ľ–ł {5/2}). [1] –ú–į—Ē —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ—É –ĺ–Ņ—É–ļ–Ľ—É –ī—Ė–Ľ—Ź–Ĺ–ļ—É –ļ–ĺ–∂–Ĺ–ĺ—ó –≥—Ä–į–Ĺ—Ė, ¬ę–Ņ—Ä–ł—Ö–ĺ–≤–į–ŗɬĽ –≤—Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—Ė, –Ņ—Ä–ł —Ü—Ć–ĺ–ľ—É –∑–ĺ–≤–Ĺ—Ė –≤–ł–ī–Ĺ–ĺ —ā—Ė–Ľ—Ć–ļ–ł —á–į—Ā—ā–ł–Ĺ—É –≥—Ä–į–Ĺ–Ķ–Ļ —É –≤–ł–≥–Ľ—Ź–ī—Ė —Ä—Ė–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–ł—Ö —ā—Ä–ł–ļ—É—ā–Ĺ—Ė–ł–ļ—Ė–≤. –ß–į—Ā—ā–ł–Ĺ–į –≥—Ä–į–Ĺ–Ķ–Ļ, —Č–ĺ –∑–Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –≤—Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—Ė –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į –≤—Ė–ī—Ė–≥—Ä–į—Ē —Ä–ĺ–Ľ—Ć –Ņ–Ľ–ĺ—Ā–ļ–ĺ—ó –ľ–Ķ–ľ–Ī—Ä–į–Ĺ–ł —ā–į –Ĺ–Ķ —Ä–ĺ–∑–ľ–Ķ–∂–ĺ–≤—É—Ē –≤–Ĺ—É—ā—Ä—Ė—ą–Ĺ—Ė–Ļ –Ņ—Ä–ĺ—Ā—ā—Ė—Ä –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į. –†–ĺ–∑—ā–į—ą—É–≤–į–Ĺ–Ĺ—Ź –≤–Ķ—Ä—ą–ł–Ĺ[en] –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į —ā–į–ļ–Ķ –∂ —Ź–ļ —Ė —É –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ė–ļ–ĺ—Ā–į–Ķ–ī—Ä–į (—ā–ĺ–Ī—ā–ĺ –ĺ–Ņ—É–ļ–Ľ–į –ĺ–Ī–ĺ–Ľ–ĺ–Ĺ–ļ–į –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į —Ē –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ł–ľ —Ė–ļ–ĺ—Ā–į–Ķ–ī—Ä–ĺ–ľ). –ź —Ä–ĺ–∑—ā–į—ą—É–≤–į–Ĺ–Ĺ—Ź —Ä–Ķ–Ī–Ķ—Ä –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į —ā–į–ļ–Ķ –∂ —Ź–ļ —Ė —É –≤–Ķ–Ľ–ł–ļ–ĺ–≥–ĺ —Ė–ļ–ĺ—Ā–į–Ķ–ī—Ä–į. –ú–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä –ľ–į—Ē –Ņ–ĺ–≤–Ĺ—É —Ā–ł–ľ–Ķ—ā—Ä—Ė—é –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ė–ļ–ĺ—Ā–į–Ķ–ī—Ä–į, —Ė –ĺ—ā–∂–Ķ, –≤—Ā—Ė –Ļ–ĺ–≥–ĺ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó, –į —Ā–į–ľ–Ķ: 1) –ľ–į—Ē 31 –≤—Ė—Ā—Ć –ĺ–Ī–Ķ—Ä—ā–ĺ–≤–ĺ—ó —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó: ‚Äí 6 –ĺ—Ā–Ķ–Ļ 5-–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ—É ‚ÄĒ –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—ā—Ć —á–Ķ—Ä–Ķ–∑ –Ņ—Ä–ĺ—ā–ł–Ľ–Ķ–∂–Ĺ—Ė –≤–Ķ—Ä—ą–ł–Ĺ–ł; ‚Äí 10 –ĺ—Ā–Ķ–Ļ 3-–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ—É ‚ÄĒ –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—ā—Ć —á–Ķ—Ä–Ķ–∑ –Ņ—Ä–ĺ—ā–ł–Ľ–Ķ–∂–Ĺ—Ė —ā–ĺ—á–ļ–ł, –≤ —Ź–ļ–ł—Ö –Ņ–Ķ—Ä–Ķ—ā–ł–Ĺ–į—é—ā—Ć—Ā—Ź –Ņ–ĺ —ā—Ä–ł –≥—Ä–į–Ĺ—Ė; ‚Äí 15 –ĺ—Ā–Ķ–Ļ 2-–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ—É ‚ÄĒ –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—ā—Ć —á–Ķ—Ä–Ķ–∑ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–ł –Ņ—Ä–ĺ—ā–ł–Ľ–Ķ–∂–Ĺ–ł—Ö –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł—Ö —Ä–Ķ–Ī–Ķ—Ä. 2) –ľ–į—Ē 15 –Ņ–Ľ–ĺ—Č–ł–Ĺ –ī–∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ—ó —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó, —Č–ĺ –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—ā—Ć —á–Ķ—Ä–Ķ–∑ –ļ–ĺ–∂–Ĺ—Ė –ī–≤—Ė —Ā—É—Ā—Ė–ī–Ĺ—Ė –≤–Ķ—Ä—ą–ł–Ĺ–ł —ā–į —Ü–Ķ–Ĺ—ā—Ä –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į (—á–Ķ—Ä–Ķ–∑ –ļ–ĺ–∂–Ĺ—É –Ņ–į—Ä—É –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł—Ö —Ä–Ķ–Ī–Ķ—Ä). 3) –ľ–į—Ē —Ü–Ķ–Ĺ—ā—Ä —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó. –Į–ļ –∑—Ė—Ä—á–į—Ā—ā–į —Ą–ĺ—Ä–ľ–į –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į
–ú–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä —Ē –Ņ–Ķ—Ä—ą–ĺ—é –∑—Ė—Ä—á–į—Ā—ā–ĺ—é —Ą–ĺ—Ä–ľ–ĺ—é –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į. –ô–ĺ–≥–ĺ –≥—Ä–į–Ĺ—Ė —Ā–ļ–Ľ–į–ī–Ķ–Ĺ—Ė –∑ –Ĺ—É–Ľ—Ć–ĺ–≤–ĺ–≥–ĺ —ā–į –Ņ–Ķ—Ä—ą–ĺ–≥–ĺ –≤—Ė–ī—Ā—Ė–ļ—Ė–≤ –Ĺ–į –ī—Ė–į–≥—Ä–į–ľ—Ė –∑–∑—Ė—Ä—á–Ķ–Ĺ–Ĺ—Ź –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į. [3] –ú–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä —É—ā–≤–ĺ—Ä—é—Ē—ā—Ć—Ā—Ź –∑ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –Ņ—Ä–ł –Ņ—Ä–ĺ–ī–ĺ–≤–∂–Ķ–Ĺ–Ĺ—Ė –Ļ–ĺ–≥–ĺ —Ä–Ķ–Ī–Ķ—Ä –ī–ĺ —ó—Ö –≤–∑–į—Ē–ľ–Ĺ–ĺ–≥–ĺ –Ņ–Ķ—Ä–Ķ—ā–ł–Ĺ—É, —ā–ĺ–Ī—ā–ĺ –ļ–ĺ–∂–Ĺ–į –≥—Ä–į–Ĺ—Ć őĪ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –∑–į–ľ—Ė–Ĺ—é—Ē—ā—Ć—Ā—Ź –∑—Ė—Ä—á–į—Ā—ā–ł–ľ –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ–ĺ–ľ –∑ —Ź–ī—Ä–ĺ–ľ őĪ.[4]
–Į–ļ –Ĺ–į—Ä–ĺ—Č–Ķ–Ĺ–Ĺ—Ź –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į–ß–į—Ā—ā–ĺ –ľ–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —Ź–ļ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ, —É—ā–≤–ĺ—Ä–Ķ–Ĺ–ł–Ļ –Ĺ–į—Ä–ĺ—Č–Ķ–Ĺ–Ĺ—Ź–ľ –Ĺ–į –≥—Ä–į–Ĺ—Ź—Ö –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ł—Ö –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł—Ö –Ņ—Ė—Ä–į–ľ—Ė–ī. –°–į–ľ –ô–ĺ–≥–į–Ĺ–Ĺ –ö–Ķ–Ņ–Ľ–Ķ—Ä –Ĺ–į–∑–ł–≤–į—Ē —Ü–Ķ–Ļ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ (–ľ–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä) –Ĺ–į—Ä–ĺ—Č–Ķ–Ĺ–ł–ľ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–ĺ–ľ (–į –Ņ—Ė–∑–Ĺ—Ė—ą–Ķ Echinus)[9]. –¶–Ķ –Ĺ–Ķ–ļ–ĺ—Ä–Ķ–ļ—ā–Ĺ–Ķ –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —Ė–Ĺ–ĺ–ī—Ė –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—Ē—ā—Ć—Ā—Ź –Ļ –ī–ĺ —Ü—Ć–ĺ–≥–ĺ —á–į—Ā—É. –Ě–į–Ņ—Ä–ł–ļ–Ľ–į–ī, MathWorld —Ā—ā–≤–Ķ—Ä–ī–∂—É—Ē, —Č–ĺ –ľ–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä –ľ–ĺ–∂–Ķ –Ī—É—ā–ł –ĺ—ā—Ä–ł–ľ–į–Ĺ–ł–Ļ —ą–Ľ—Ź—Ö–ĺ–ľ –ī–ĺ–ī–į–≤–į–Ĺ–Ĺ—Ź –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ł—Ö –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł—Ö –Ņ—Ė—Ä–į–ľ—Ė–ī –ī–ĺ –≥—Ä–į–Ĺ–Ķ–Ļ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į.[10] –ě–ī–Ĺ–į–ļ —Ü–Ķ —ā–≤–Ķ—Ä–ī–∂–Ķ–Ĺ–Ĺ—Ź –Ņ—Ä–ł–ī–į—ā–Ĺ–Ķ –Ľ–ł—ą–Ķ –ī–Ľ—Ź –Ņ–ĺ–Ľ–Ķ–≥—ą–Ķ–Ĺ–Ĺ—Ź –≤—Ė–∑—É–į–Ľ—Ė–∑–į—Ü—Ė—ó —Ü—Ć–ĺ–≥–ĺ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į, –į–Ī–ĺ –ī–Ľ—Ź –≤–ł–≥–ĺ—ā–ĺ–≤–Ľ–Ķ–Ĺ–Ĺ—Ź –Ļ–ĺ–≥–ĺ –Ņ–į–Ņ–Ķ—Ä–ĺ–≤–ĺ—ó –ľ–ĺ–ī–Ķ–Ľ—Ė, –į–Ī–ĺ –ī–Ľ—Ź –ĺ–Ī—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—Ź –Ļ–ĺ–≥–ĺ —Ä–ĺ–∑–ľ—Ė—Ä—Ė–≤, –į–Ľ–Ķ –Ĺ–Ķ –ī–Ľ—Ź –Ļ–ĺ–≥–ĺ –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —Ź–ļ —ā—Ė–Ľ–į, —ā–į–ļ —Ź–ļ –Ņ—Ä–ł –Ņ—Ä–ł—Ē–ī–Ĺ–į–Ĺ–Ĺ—Ė (–Ĺ–į—Ä–ĺ—Č–Ķ–Ĺ–Ĺ—Ė) –Ņ—Ė—Ä–į–ľ—Ė–ī (–∑ –Ī–ĺ–ļ–ĺ–≤–ł–ľ–ł –≥—Ä–į–Ĺ—Ź–ľ–ł ‚ÄĒ –∑–ĺ–Ľ–ĺ—ā–ł–ľ–ł —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į–ľ–ł) –ī–ĺ –≥—Ä–į–Ĺ–Ķ–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į, –≤ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ—É –Ņ—Ä–ł—Ā—É—ā–Ĺ—Ė ¬ę—Ö–ł–Ī–Ĺ—Ė¬Ľ –≤–Ķ—Ä—ą–ł–Ĺ–ł (—ā—Ė, —Č–ĺ –∑–Ĺ–į—Ö–ĺ–ī—Ź—ā—Ć—Ā—Ź –Ĺ–į –Ņ–Ķ—Ä–Ķ—ā–ł–Ĺ—Ė —Ä–Ķ–Ī–Ķ—Ä), —Ź–ļ—Ė –Ĺ–į—Ā–Ņ—Ä–į–≤–ī—Ė –Ĺ–Ķ —Ē –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į, –į —ā–į–ļ–ĺ–∂ –ī–ĺ–ī–į—ā–ļ–ĺ–≤—Ė —Ä–Ķ–Ī—Ä–į (–ī–≤–į —Ä–Ķ–Ī—Ä–į –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł—Ö –Ņ—Ė—Ä–į–ľ—Ė–ī —ā–į –ĺ–ī–Ĺ–Ķ —Ä–Ķ–Ī—Ä–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –Ľ–Ķ–∂–į—ā—Ć –Ĺ–į –ĺ–ī–Ĺ—Ė–Ļ –Ņ—Ä—Ź–ľ—Ė–Ļ —Ė –≤—Ė–∑—É–į–Ľ—Ć–Ĺ–ĺ —Ā—ā–≤–ĺ—Ä—é—é—ā—Ć –≤—Ä–į–∂–Ķ–Ĺ–Ĺ—Ź –ĺ–ī–Ĺ–ĺ–≥–ĺ —Ä–Ķ–Ī—Ä–į). –Ď–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ, —É—ā–≤–ĺ—Ä–Ķ–Ĺ–ł–Ļ —ą–Ľ—Ź—Ö–ĺ–ľ –Ņ—Ä–ł—Ē–ī–Ĺ–į–Ĺ–Ĺ—Ź –Ņ—Ä—Ź–ľ–ł—Ö –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł—Ö –Ņ—Ė—Ä–į–ľ—Ė–ī –ī–ĺ –≥—Ä–į–Ĺ–Ķ–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į, —Ē —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥—Ė—á–Ĺ–ĺ –Ķ–ļ–≤—Ė–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ł–ľ –ī–ĺ –Ņ–Ķ–Ĺ—ā–į–ļ—Ė—Ā–ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į[en] (–ĺ–ī–Ĺ–ĺ–≥–ĺ –∑ —ā—Ė–Ľ –ö–į—ā–į–Ľ–į–Ĺ–į), —ā–į –Ĺ–Ķ —Ē –ľ–į–Ľ–ł–ľ –∑—Ė—Ä—á–į—Ā—ā–ł–ľ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–ĺ–ľ.
–Ę–ĺ–Ņ–ĺ–Ľ–ĺ–≥—Ė—Ź–ú–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä –ľ–į—Ē 12 –≥—Ä–į–Ĺ–Ķ–Ļ (–Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ), –Ņ—Ä–ł —Ü—Ć–ĺ–ľ—É —Ü—Ė –Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ–ł —Ä–Ķ—Ä–Ķ—ā–ł–Ĺ–į—é—ā—Ć—Ā—Ź –Ņ–ĺ 30 —Ä–Ķ–Ī—Ä–į—Ö –≤ 12 –≤–Ķ—Ä—ą–ł–Ĺ–į—Ö. –ě—ā–∂–Ķ, –Ļ–ĺ–≥–ĺ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–į –ē–Ļ–Ľ–Ķ—Ä–į –ľ–į—Ē –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź , —Ė –ľ–ł –ľ–ĺ–∂–Ķ–ľ–ĺ –ĺ–Ī—á–ł—Ā–Ľ–ł—ā–ł –Ļ–ĺ–≥–ĺ —Ä—Ė–ī –∑–į –ī–ĺ–Ņ–ĺ–ľ–ĺ–≥–ĺ—é —Ą–ĺ—Ä–ľ—É–Ľ–ł –ē–Ļ–Ľ–Ķ—Ä–į:
–ě—ā–∂–Ķ, . –ó–≤—Ė–ī–ļ–ł –≤–ł–Ņ–Ľ–ł–≤–į—Ē, —Č–ĺ –ľ–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä –ľ–į—Ē —Ä—Ė–ī . –¶–Ķ —Ā–Ņ–ĺ—Ā—ā–Ķ—Ä–Ķ–∂–Ķ–Ĺ–Ĺ—Ź, –∑—Ä–ĺ–Ī–Ľ–Ķ–Ĺ–Ķ –õ—É—ó –ü—É–į–Ĺ—Ā–ĺ, —Ā–Ņ–ĺ—á–į—ā–ļ—É –≤–ł–ļ–Ľ–ł–ļ–į–Ľ–ĺ –Ņ–Ľ—É—ā–į–Ĺ–ł–Ĺ—É, –į–Ľ–Ķ –§–Ķ–Ľ—Ė–ļ—Ā –ö–Ľ—Ź–Ļ–Ĺ –Ņ–ĺ–ļ–į–∑–į–≤ —É 1877 —Ä–ĺ—Ü—Ė, —Č–ĺ –ľ–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä –ľ–ĺ–∂–Ĺ–į —Ä–ĺ–∑–≥–Ľ—Ź–ī–į—ā–ł —Ź–ļ —Ä–ĺ–∑–≥–į–Ľ—É–ī–∂–Ķ–Ĺ–Ķ –Ņ–ĺ–ļ—Ä–ł—ā—ā—Ź —Ā—Ą–Ķ—Ä–ł –†—Ė–ľ–į–Ĺ–į —Ä—Ė–ľ–į–Ĺ–ĺ–≤–ĺ—é –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–Ķ—é —Ä–ĺ–ī—É 4, –∑ —ā–ĺ—á–ļ–į–ľ–ł —Ä–ĺ–∑–≥–į–Ľ—É–∂–Ķ–Ĺ–Ĺ—Ź –≤ —Ü–Ķ–Ĺ—ā—Ä—Ė –ļ–ĺ–∂–Ĺ–ĺ—ó –Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ–ł. –Ě–į—Ā–Ņ—Ä–į–≤–ī—Ė —Ü—Ź —Ä—Ė–ľ–į–Ĺ–ĺ–≤–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ—Ź, —Ź–ļ–į –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –ļ—Ä–ł–≤–ĺ—é –Ď—Ä—Ė–Ĺ–≥–į[en], –ľ–į—Ē –Ĺ–į–Ļ–Ī—Ė–Ľ—Ć—ą—É –ļ—Ė–Ľ—Ć–ļ—Ė—Ā—ā—Ć —Ā–ł–ľ–Ķ—ā—Ä—Ė–Ļ —Ā–Ķ—Ä–Ķ–ī –Ī—É–ī—Ć-—Ź–ļ–ł—Ö —Ä—Ė–ľ–į–Ĺ–ĺ–≤–ł—Ö –Ņ–ĺ–≤–Ķ—Ä—Ö–ĺ–Ĺ—Ć —Ä–ĺ–ī—É 4: –≥—Ä—É–Ņ–į —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó –≤–ł—Ā—ā—É–Ņ–į—Ē —Ź–ļ –į–≤—ā–ĺ–ľ–ĺ—Ä—Ą—Ė–∑–ľ.[6] –§–ĺ—Ä–ľ—É–Ľ–ł –£ –≤—Ā—Ė—Ö —Ą–ĺ—Ä–ľ—É–Ľ–į—Ö –Ĺ–ł–∂—á–Ķ: ‚ÄĒ –≤—Ė–ī–Ĺ–ĺ—ą–Ķ–Ĺ–Ĺ—Ź –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü—Ė—ó ¬ę–∑–ĺ–Ľ–ĺ—ā–ĺ–≥–ĺ –Ņ–Ķ—Ä–Ķ—ā–ł–ŗɬĽ. (–Ņ–ĺ—Ā–Ľ—Ė–ī–ĺ–≤–Ĺ—Ė—Ā—ā—Ć A001622 –∑ –ě–Ĺ–Ľ–į–Ļ–Ĺ –Ķ–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī—Ė—ó –Ņ–ĺ—Ā–Ľ—Ė–ī–ĺ–≤–Ĺ–ĺ—Ā—ā–Ķ–Ļ —Ü—Ė–Ľ–ł—Ö —á–ł—Ā–Ķ–Ľ, OEIS).
–¶–Ķ–Ĺ—ā—Ä –ľ–į—Ā –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –∑–Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –≤ –Ļ–ĺ–≥–ĺ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ–ľ—É —Ü–Ķ–Ĺ—ā—Ä—Ė. –ú–ĺ–ľ–Ķ–Ĺ—ā —Ė–Ĺ–Ķ—Ä—Ü—Ė—ó —Ā—É—Ü—Ė–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –∑ –ľ–į—Ā–ĺ—é m —ā–į –ī–ĺ–≤–∂–ł–Ĺ–ĺ—é —Ä–Ķ–Ī—Ä–į a (–≤—Ė—Ā—Ć –ĺ–Ī–Ķ—Ä—ā–į–Ĺ–Ĺ—Ź –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā—Ć —á–Ķ—Ä–Ķ–∑ –Ņ—Ä–ĺ—ā–ł–Ľ–Ķ–∂–Ĺ—Ė –≤–Ķ—Ä—ą–ł–Ĺ–ł):[11]
–í–Ņ–ł—Ā–į–Ĺ–į —ā–į –Ĺ–į–Ņ—Ė–≤–≤–Ņ–ł—Ā–į–Ĺ–į —Ā—Ą–Ķ—Ä–ł –Ņ–ĺ–≤–Ĺ—Ė—Ā—ā—é –Ľ–Ķ–∂–į—ā—Ć –≤—Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—Ė –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į —ā–į –Ĺ–Ķ –≤–ł—Ö–ĺ–ī—Ź—ā—Ć –∑–į –Ļ–ĺ–≥–ĺ –ľ–Ķ–∂—Ė. –ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł –≤–Ķ—Ä—ą–ł–Ĺ –ú–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä –∑ –ī–ĺ–≤–∂–ł–Ĺ–ĺ—é —Ä–Ķ–Ī—Ä–į –≤ –ī–Ķ–ļ–į—Ä—ā–ĺ–≤—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –ľ–į—Ē –≤–Ķ—Ä—ą–ł–Ĺ–ł –∑ –Ĺ–į—Ā—ā—É–Ņ–Ĺ–ł–ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł: –ü—Ä–ł —Ü—Ć–ĺ–ľ—É –≤–Ķ—Ä—ą–ł–Ĺ–ł –Ľ–Ķ–∂–į—ā—Ć –≤ —á–ĺ—ā–ł—Ä—Ć–ĺ—Ö –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł—Ö –Ņ–Ľ–ĺ—Č–ł–Ĺ–į—Ö (–Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł—Ö –ī–ĺ –Ņ–Ľ–ĺ—Č–ł–Ĺ–ł Oxy), –≤ –ļ–ĺ–∂–Ĺ—Ė–Ļ –∑ —Ź–ļ–ł—Ö —Ä–ĺ–∑—ā–į—ą–ĺ–≤–į–Ĺ—Ė —Ź–ļ –≤–Ķ—Ä—ą–ł–Ĺ–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–ł–ļ—É—ā–Ĺ–ł–ļ–į. –ü–ĺ—á–į—ā–ĺ–ļ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į, —Č–ĺ —Ē –Ļ–ĺ–≥–ĺ —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó —ā–į —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤–Ņ–ł—Ā–į–Ĺ–ĺ—ó, –Ĺ–į–Ņ—Ė–≤–≤–Ņ–ł—Ā–į–Ĺ–ĺ—ó —ā–į –ĺ–Ņ–ł—Ā–į–Ĺ–ĺ—ó —Ā—Ą–Ķ—Ä. –í—Ė—Ā—Ć Oz –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ –ĺ–ī–Ĺ—Ė—Ē—é –∑ –ĺ—Ā–Ķ–Ļ —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó 3-–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ—É, –į –≤—Ė—Ā—Ć Oy ‚ÄĒ –∑ –ĺ–ī–Ĺ—Ė—Ē—é –∑ –ĺ—Ā–Ķ–Ļ —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó 2-–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ—É. –ü–Ľ–ĺ—Č–ł–Ĺ–į Oxz –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ –ĺ–ī–Ĺ—Ė—Ē—é –∑ –Ņ–Ľ–ĺ—Č–ł–Ĺ —Ā–ł–ľ–Ķ—ā—Ä—Ė—ó –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į. –ü–ĺ–≤'—Ź–∑–į–Ĺ—Ė —ā–į —Ā–Ņ–ĺ—Ä—Ė–ī–Ĺ–Ķ–Ĺ—Ė –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–ł–ě–Ņ—É–ļ–Ľ–į –ĺ–Ī–ĺ–Ľ–ĺ–Ĺ–ļ–į –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į —Ē –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ł–ľ —Ė–ļ–ĺ—Ā–į–Ķ–ī—Ä–ĺ–ľ. –†–Ķ–Ī—Ä–į –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –∑–Ī—Ė–≥–į—é—ā—Ć—Ā—Ź –∑ —Ä–Ķ–Ī—Ä–į–ľ–ł –≤–Ķ–Ľ–ł–ļ–ĺ–≥–ĺ —Ė–ļ–ĺ—Ā–į–Ķ–ī—Ä–į; –Ņ–ĺ—Ē–ī–Ĺ–į–Ĺ–Ĺ—Ź —Ü–ł—Ö –ī–≤–ĺ—Ö –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ—Ė–≤ —É—ā–≤–ĺ—Ä—é—Ē –≤–ł—Ä–ĺ–ī–∂–Ķ–Ĺ–ł–Ļ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ, —Č–ĺ –ľ–į—Ē –Ĺ–į–∑–≤—É –≤–Ķ–Ľ–ł–ļ–ł–Ļ —Ā–ļ–Ľ–į–ī–Ķ–Ĺ–ł–Ļ —Ė–ļ–ĺ—Ā–ĺ–ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä[en].  –Ü—Ā–Ĺ—É—Ē —á–ĺ—ā–ł—Ä–ł –Ĺ–Ķ–ĺ–Ņ—É–ļ–Ľ–ł—Ö –ĺ–ī–Ĺ–ĺ—Ä—Ė–ī–Ĺ–ł—Ö –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ—Ė–≤, —Č–ĺ —É—ā–≤–ĺ—Ä–Ķ–Ĺ—Ė –Ņ–Ķ–≤–Ĺ–ł–ľ–ł —Ā—ā—É–Ņ–Ķ–Ĺ—Ź–ľ–ł –ĺ–Ņ–Ķ—Ä–į—Ü—Ė—ó –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ź –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į. –ó—Ä—Ė–∑–į–Ĺ–ł–Ļ –ľ–į–Ľ–ł–Ļ –∑—Ė—Ä—á–į—Ā—ā–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä –ľ–ĺ–∂–Ĺ–į –≤–≤–į–∂–į—ā–ł –≤–ł—Ä–ĺ–ī–∂–Ķ–Ĺ–ł–ľ –ĺ–ī–Ĺ–ĺ—Ä—Ė–ī–Ĺ–ł–ľ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–ĺ–ľ. –í–Ķ—Ä—ą–ł–Ĺ–ł –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –∑—Ä—Ė–∑–į—é—ā—Ć—Ā—Ź, –Ņ–ĺ–ļ–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā –Ĺ–Ķ –ī–ĺ—Ā—Ź–≥–į—Ē –Ņ–Ľ–ĺ—Č–ł–Ĺ –Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ –Ņ—Ė–ī –Ĺ–ł–ľ–ł. –í—Ė–∑—É–į–Ľ—Ć–Ĺ–ĺ –≤—Ė–Ĺ –≤–ł–≥–Ľ—Ź–ī–į—Ē —Ź–ļ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä, –į–Ľ–Ķ –ľ–į—Ē 24 –Ņ–ĺ–ī–≤—Ė–Ļ–Ĺ–ĺ-–Ĺ–į–ļ—Ä–ł—ā—Ė –≥—Ä–į–Ĺ—Ė ‚ÄĒ 12 –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤, —É—ā–≤–ĺ—Ä–Ķ–Ĺ–ł—Ö –≤—Ė–ī –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ź –≤–Ķ—Ä—ą–ł–Ĺ —Ė 12 –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤, —É—ā–≤–ĺ—Ä–Ķ–Ĺ–ł—Ö –≤—Ė–ī –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ź –Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ, —Ź–ļ—Ė –Ņ–Ķ—Ä–Ķ–ļ—Ä–ł–≤–į—é—ā—Ć –Ņ–Ķ—Ä—ą—Ė 12 –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤. –ü'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ–ł —Ė–∑ –∑—Ä—Ė–∑–į–Ĺ–ł—Ö –Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ –Ĺ–į—Ā–Ņ—Ä–į–≤–ī—Ė —Ē –≤–ł—Ä–ĺ–ī–∂–Ķ–Ĺ–ł–ľ–ł –ī–Ķ—Ā—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ–į–ľ–ł {10/2}, —Č–ĺ –Ņ—Ä–ł–Ļ–ľ–į—é—ā—Ć —Ą–ĺ—Ä–ľ—É –Ņ–ĺ–ī–≤—Ė–Ļ–Ĺ–ĺ-–Ĺ–į–ļ—Ä–ł—ā–ł—Ö –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ—Ė–≤ —Ė–∑ –ī–≤–ĺ–ľ–į –ľ–Ĺ–ĺ–∂–ł–Ĺ–į–ľ–ł –≤–Ķ—Ä—ą–ł–Ĺ —Ė —Ä–Ķ–Ī–Ķ—Ä, –Ĺ–į–ļ–Ľ–į–ī–Ķ–Ĺ–ł—Ö –ĺ–ī–Ĺ–Ķ –Ĺ–į –ĺ–ī–Ĺ–Ķ. –ö–ĺ–Ľ–ł n‚ĀĄd -–ļ—É—ā–Ĺ–ł–ļ —Ā–ļ–ĺ—Ä–ĺ—á—É—Ē—ā—Ć—Ā—Ź –≤ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ė –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ź, –≤—Ė–Ĺ —Ā—ā–į—Ē 2n‚ĀĄd -–ļ—É—ā–Ĺ–ł–ļ–ĺ–ľ. –Ě–į–Ņ—Ä–ł–ļ–Ľ–į–ī, –∑—Ä—Ė–∑–į–Ĺ–ł–Ļ –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ { 5‚ĀĄ1 } —Ā—ā–į—Ē –ī–Ķ—Ā—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ–ĺ–ľ { 10‚ĀĄ1 }, –į –∑—Ä—Ė–∑–į–Ĺ–į –Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ–į { 5‚ĀĄ2 } —Ā—ā–į—Ē –Ņ–ĺ–ī–≤—Ė–Ļ–Ĺ–ĺ-–Ĺ–į–ļ—Ä–ł—ā–ł–ľ –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ–ĺ–ľ (—ā–ĺ–Ī—ā–ĺ –ī–Ķ—Ā—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ–ĺ–ľ, —Č–ĺ –ľ–į—Ē —Ą–ĺ—Ä–ľ—É –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ–į) { 10‚ĀĄ2 } (—Ü–Ķ –ĺ–∑–Ĺ–į—á–į—Ē, —Č–ĺ –ľ–ł –≤—Ė–ī–≤—Ė–ī–į—Ē–ľ–ĺ –ļ–ĺ–∂–Ĺ—É –≤–Ķ—Ä—ą–ł–Ĺ—É –ī–≤—Ė—á—Ė, —Č–ĺ–Ī –∑–į–≤–Ķ—Ä—ą–ł—ā–ł –Ī–į–≥–į—ā–ĺ–ļ—É—ā–Ĺ–ł–ļ). –Ď–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ –ľ–į—Ē 60 –≤–Ķ—Ä—ą–ł–Ĺ (–≤ –ļ–ĺ–∂–Ĺ—Ė–Ļ –≤–Ķ—Ä—ą–ł–Ĺ—Ė ¬ę–ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į¬Ľ –ľ—Ė—Ā—ā—Ź—ā—Ć—Ā—Ź —ā—Ä–ł –≤–Ķ—Ä—ą–ł–Ĺ–ł –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į) —ā–į 90 —Ä–Ķ–Ī–Ķ—Ä (–ļ–ĺ–∂–Ĺ–Ķ —Ä–Ķ–Ī—Ä–ĺ ¬ę–ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į¬Ľ —Ē –Ņ–ĺ—ā—Ä—Ė–Ļ–Ĺ–ł–ľ ‚ÄĒ –ĺ–ī–Ĺ–Ķ —Ä–Ķ–Ī—Ä–ĺ –≤—Ė–ī –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ź –≤–Ķ—Ä—ą–ł–Ĺ–ł (–≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–į —Ą—Ė–≥—É—Ä–į ‚ÄĒ –ĺ–Ņ—É–ļ–Ľ–ł–Ļ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ł–Ļ –Ņ'—Ź—ā–ł–ļ—É—ā–Ĺ–ł–ļ) —ā–į –ī–≤–į —Ä–Ķ–Ī—Ä–į –≤—Ė–ī –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ź –Ņ–Ķ–Ĺ—ā–į–≥—Ä–į–ľ–ł).
–Ē–ĺ–ī–Ķ–ļ–į–ī–ĺ–ī–Ķ–ļ–į–ī—Ä[en] —É—ā–≤–ĺ—Ä—é—Ē—ā—Ć—Ā—Ź –Ņ—Ä–ł –Ņ–ĺ–≤–Ĺ–ĺ–ľ—É –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ė[en] (—Ä–Ķ–ļ—ā–ł—Ą—Ė–ļ–į—Ü—Ė—ó) –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į, –ļ–ĺ–Ľ–ł –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ź –≤–Ķ—Ä—ą–ł–Ĺ –Ņ—Ä–ĺ–≤–ĺ–ī–ł—ā—Ć—Ā—Ź –ī–ĺ —ā–ĺ—á–ĺ–ļ, —Č–ĺ –Ľ–Ķ–∂–į—ā—Ć –Ĺ–į —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į—Ö —Ä–Ķ–Ī–Ķ—Ä –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į, —ā–ĺ–Ī—ā–ĺ —Ä–Ķ–Ī—Ä–į –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–ĺ–≥–ĺ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į —Ą–į–ļ—ā–ł—á–Ĺ–ĺ –∑–Ĺ–ł–ļ–į—é—ā—Ć.
–ó—Ä—Ė–∑–į–Ĺ–ł–Ļ –≤–Ķ–Ľ–ł–ļ–ł–Ļ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä[en] —Ē –ĺ–ī–Ĺ–ĺ—Ä—Ė–ī–Ĺ–ł–ľ –Ĺ–Ķ–ĺ–Ņ—É–ļ–Ľ–ł–ľ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–ĺ–ľ U37, —Č–ĺ –ľ–į—Ē –ī—Ė–į–≥—Ä–į–ľ—É –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į ‚ÄĒ –Ē–ł–Ĺ–ļ—Ė–Ĺ–į –ü—Ä–ĺ—Ü–Ķ—Ā –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ź –ľ–į–Ľ–ĺ–≥–ĺ –∑—Ė—Ä—á–į—Ā—ā–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į –∑–į–≤–Ķ—Ä—ą—É—Ē—ā—Ć—Ā—Ź (–Ņ—Ä–ł –Ņ–ĺ–≤–Ĺ–ĺ–ľ—É –≥–Ľ–ł–Ī–ĺ–ļ–ĺ–ľ—É –∑—Ä—Ė–∑–į–Ĺ–Ĺ—Ė –į–Ī–ĺ –Ī—Ė—Ä–Ķ–ļ—ā–ł—Ą—Ė–ļ–į—Ü—Ė—ó) —É—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź–ľ –ī–≤–ĺ—ó—Ā—ā–ĺ–≥–ĺ –ī–ĺ –Ĺ—Ć–ĺ–≥–ĺ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į ‚ÄĒ –≤–Ķ–Ľ–ł–ļ–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į, –ļ–ĺ–Ľ–ł –≥—Ä–į–Ĺ—Ė –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–ĺ–≥–ĺ –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–į –∑–ľ–Ķ–Ĺ—ą—É—é—ā—Ć—Ā—Ź –ī–ĺ —ā–ĺ—á–ĺ–ļ, —ā–ĺ–Ī—ā–ĺ —Ą–į–ļ—ā–ł—á–Ĺ–ĺ –∑–Ĺ–ł–ļ–į—é—ā—Ć.
–†–ĺ–ī–ł–Ĺ–į –∑—Ė—Ä—á–į—Ā—ā–ł—Ö —Ą–ĺ—Ä–ľ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä–į.
  –Ē–≤–į –ĺ–ī–Ĺ–ĺ—Ä—Ė–ī–Ĺ–ł—Ö –∑'—Ē–ī–Ĺ–į–Ĺ–Ĺ—Ź –Ī–į–≥–į—ā–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ—Ė–≤ —Ā–ļ–Ľ–į–ī–į—é—ā—Ć—Ā—Ź –∑ –ľ–į–Ľ–ł—Ö –∑—Ė—Ä—á–į—Ā—ā–ł—Ö –ī–ĺ–ī–Ķ–ļ–į–Ķ–ī—Ä—Ė–≤:
–Ē–ĺ–ī–į—ā–ļ–ĺ–≤–ĺ
–í –ľ–ł—Ā—ā–Ķ—Ü—ā–≤—Ė —ā–į –į—Ä—Ö—Ė—ā–Ķ–ļ—ā—É—Ä—Ė
–Ē–ł–≤. —ā–į–ļ–ĺ–∂
–ü—Ä–ł–ľ—Ė—ā–ļ–ł
–õ—Ė—ā–Ķ—Ä–į—ā—É—Ä–į
–ü–ĺ—Ā–ł–Ľ–į–Ĺ–Ĺ—Ź
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia